I What is the gravitational component in the radial direction?

[SebastianRM]

Hey guys, I reading over Taylor's Classical Mechanics book. Chapter 9, Centrifugal Acceleration Section.
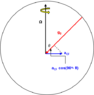
In p.346 he mentions that for a free fall acceleration:
g = g_0 + Ω^2 * Rsinθ ρ
Where its radial component would be:
g_rad = g_0 - Ω^2 * Rsinθ^2
I am just confused in the derivation, I am unsure of how he got there.

 

[kuruman]

The first equation you posted adds the centrifugal component to the force of attraction between the Earth and the mass. That is explained in Eq. (9.43). The second equation you posted is the magnitude of the vector sum implied by the first equation (see exaggerated diagram below). Taylor is calculating the radial component of the effective g (black arrow). This is the red arrow plus the projection of the centrifugal force F_CF on the red arrow. That's $F_{CF}\sin \theta$. $F_{CF}$ itself is given in Eq. (9.40).

 

[SebastianRM]

I am a bit confused on the projection aspect, I can only recall projection involving cos(theta) so would you mind explaining how to derive that projection?

 

[jbriggs444]

I am a bit confused on the projection aspect, I can only recall projection involving cos(theta) so would you mind explaining how to derive that projection?

If you take an angle theta in the first quadrant, the projection on the x-axis involves cos(theta). Its projection on the y-axis involves sin(theta).

Here, if we imagine coordinate axes, we could lay down the x-axis tangential to the Earth's surface (running from northwest to southeast). We could then lay down the y-axis at right angles, running from the center of the Earth out to the point of tangency. Now F_CF is in the first quadrant and we want the projection on the y-axis (i.e. parallel to gravity). So we use the sine.

We could measure a different angle, e.g. the angle between F_CF and g₀. The projection would involve the cosine of that angle. Both sine and cosine are correct because the two angles are complementary (add up to 90 degrees).

 

[kuruman]

Both sine and cosine are correct because the two angles are complementary (add up to 90 degrees).

Yes but Taylor's textbook measures angle $\theta$ from the Earth's rotation axis which in the drawing is from the bottom of the screen to the top (colatitude). The acute angle between the magnitudes of the red vector and the blue vector is 90^o - θ. The choice has already been made.

 

[SebastianRM]

Yes but Taylor's textbook measures angle $\theta$ from the Earth's rotation axis which in the drawing is from the bottom of the screen to the top (colatitude). The acute angle between the magnitude of the red vector and the blue vector is 90^o - θ. The choice has already been made.

Would you guys mind doing a diagram for this? I do not know why I am not getting it. I tried doing a diagram myself, I ended up with an X looking diagram with x-axis going from NW to SE (having this shape \ ). And the y-axis would be this element: / (So g_0 is pointing along this axis). With an angle theta between the y-axis and the Earth's rotation axis. This means that 90-theta will be the angle between g_0 and F_cf . That also means that the angle between F_cf and x-axis is also 90-theta.
So the projection of F_cf on the y-axis would be F_cf sin(90-theta), which i think it wrong it should only be F_cf sin(theta).

 

[kuruman]

Would you guys mind doing a diagram for this?

The radial component (in the $-\hat r$ direction) of the vector sum of red and blue is $g_0-a_{CF}\cos(90^o-\theta)= g_0-a_{CF}\sin \theta$. The magnitude of the centripetal acceleration is $a_{CF}=\Omega^2\rho=\Omega^2R \sin \theta$ (see fig. 9.9).