What is the lapse rate in a simplified model of cloud formation?

[Saitama]

Homework Statement

Consider a simplified model of cloud formation. Hot air in contact with the earth’s surface contains water vapor. This air rises convectively till the water vapor content reaches its saturation pressure. When this happens, the water vapor starts condensing and droplets are formed. We shall estimate the height at which this happens. We assume that the atmosphere consists of the diatomic gases oxygen and nitrogen in the mass proportion 21:79 respectively. We further assume that the atmosphere is an ideal gas, g the acceleration due to gravity is constant and air processes are adiabatic. Under these assumptions one can show that the pressure is given by
$$p=p_0\left(\frac{T_0-\Gamma z}{T_0}\right)^{\alpha}$$
Here $p_0$ and $T_0$ is the pressure and temperature respectively at sea level $(z = 0)$, $\Gamma$ is the lapse rate (magnitude of the change in temperature $T$ with height $z$ above the earth’s surface, i.e. $\Gamma > 0$).

(a) Obtain an expression for the lapse rate $\Gamma$ in terms of $\gamma, R, g$ and $m_a$. Here $\gamma$ is the ratio of specific heat at constant pressure to specific heat at constant volume; $R$, the gas constant; and $m_a$, the relevant molar mass.

(There are few more parts to this problem, they seem to be related to (a), I will post them when I solve a) ).

Homework Equations

The Attempt at a Solution

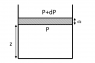
Consider a layer at height $z$, cross section $A$ and thickness $dz$. Let $p$ and $p+dp$ be the pressure on two sides as shown in figure. The mass of the air in this layer is $A\rho \,dz$ where $\rho$ is the density of air at height $z$. Equating the forces, I get
$$\frac{dp}{dz}=-\rho g$$
Now I am not sure what to do after this. From the ideal gas, I have $\rho=(pm_a)/(RT)$ but how do I introduce $\gamma$?

Is my approach even correct?

Any help is appreciated. Thanks!

 

[voko]

The key assumption in deriving the lapse rate is that when air rises, it expands, does work, and cools down.

 

[Saitama]

Hi voko!

The key assumption in deriving the lapse rate is that when air rises, it expands, does work, and cools down.

How do you conclude this from the problem statement? And how do I make the equations? Do I have to use $PV^{\gamma}=\text{constant}$?

 

[voko]

The statement is a bit obscure in this respect, but the following is consistent with what I said: "This air rises convectively"; "air processes are adiabatic".

Your equation is a good starting point.

 

[Saitama]

The statement is a bit obscure in this respect, but the following is consistent with what I said: "This air rises convectively"; "air processes are adiabatic".

Your equation is a good starting point.

Let the initial pressure be $P$ and volume occupied be $Az$. When the gas expands by height $dz$, I have:
$$P(Az)^{\gamma}=(P+dP)(A(z+dz))^{\gamma} \Rightarrow P=(P+dP)\left(1+\frac{dz}{z}\right)^{\gamma} \approx (P+dP)\left(1+\gamma\frac{dz}{z}\right)$$
$$\Rightarrow \frac{dP}{dz}=-\gamma \frac{P}{z}$$

Is this correct?

 

[voko]

No, that is not correct. You assumed that $A$ was constant, but there is no reason to assume that. Besides, you obtained the relationship between $p$ and $z$ in #1; it is good. What you need here is a relationship between $T$ and $p$.

 

[Chestermiller]

How is the temperature related to the pressure in the adiabatic reversible expansion of an ideal gas?

 

[Saitama]

No, that is not correct. You assumed that $A$ was constant, but there is no reason to assume that. Besides, you obtained the relationship between $p$ and $z$ in #1; it is good. What you need here is a relationship between $T$ and $p$.

How is the temperature related to the pressure in the adiabatic reversible expansion of an ideal gas?

$$PT^{\gamma/(1-\gamma)}=\text{constant}$$

But how to make use of this?

 

[voko]

You have two equations: one linking $p$ and $z$, another linking $p$ and $T$. You need to find $\Gamma(z) = - T'(z)$.

 

[Saitama]

You have two equations: one linking $p$ and $z$, another linking $p$ and $T$. You need to find $\Gamma(z) = - T'(z)$.

I differentiate the equation relating p and T with respect to z.
$$T^{\gamma/(1-\gamma)}\,\frac{dp}{dz}+ \frac{\gamma p}{1-\gamma}\frac{T^{\gamma/(1-\gamma)}}{T}\frac{dT}{dz}=0$$
$$\Rightarrow \frac{dp}{dz}=-\frac{\gamma}{1-\gamma} \frac{p}{T}\frac{dT}{dz}$$
Also,
$$\frac{dp}{dz}=-\frac{pm_a g}{RT}$$
Equating both, I get
$$\frac{dT}{dz}=\Gamma=\frac{m_ag}{R}\frac{1-\gamma}{\gamma}$$
But this is not correct, I have got a sign error somewhere. :(

 

[voko]

Look again at #9.

 

[Saitama]

Look again at #9.

Why a negative sign?

 

[Chestermiller]

Why a negative sign?

The sign is correct. The temperature decreases with altitude in the atmosphere. When a parcel of air rises, the pressure decreases, and the parcel expands adiabatically against the surrounding parcels, doing work. So you get expansion cooling.

 

[voko]

Why a negative sign?

Look how the lapse rate is described in your #1.

 

[Saitama]

The sign is correct. The temperature decreases with altitude in the atmosphere. When a parcel of air rises, the pressure decreases, and the parcel expands adiabatically against the surrounding parcels, doing work. So you get expansion cooling.

Look how the lapse rate is described in your #1.

Ah yes, thanks a lot both of you, the other parts have been solved too.