----md
- 3
- 0
Hi All- Hope you can help me :|
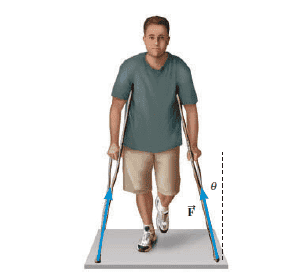
The person in the drawing is standing on crutches. Assume that the force exerted on each crutch by the ground is directed along the crutch, as the force vectors in the drawing indicate. If the coefficient of static friction between a crutch and the ground is 0.90, determine the largest angle θMAX that the crutch can have just before it begins to slip on the floor.
Fup= Fdown
Fright= Fleft
Fnet=0
I figured the for each crutch
Fy = N= 1/2mg + FcosΘ
Fx= μsN=FsinΘ
But I end up with mg and no way to eliminate it?
I know I am missing some important detail- but as with many force problems, I can't visualize it.
Thanks
Homework Statement
The person in the drawing is standing on crutches. Assume that the force exerted on each crutch by the ground is directed along the crutch, as the force vectors in the drawing indicate. If the coefficient of static friction between a crutch and the ground is 0.90, determine the largest angle θMAX that the crutch can have just before it begins to slip on the floor.
Homework Equations
Fup= Fdown
Fright= Fleft
Fnet=0
The Attempt at a Solution
I figured the for each crutch
Fy = N= 1/2mg + FcosΘ
Fx= μsN=FsinΘ
But I end up with mg and no way to eliminate it?
I know I am missing some important detail- but as with many force problems, I can't visualize it.
Thanks