What Is the Maximum Size of a Cube That Can Balance on a Cylinder?

[Saitama]

Homework Statement

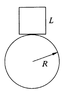
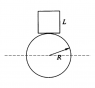
A cubical block of side L rests on a fixed cylindrical drum of radius R. Find the largest value of L for which the block is stable.

Homework Equations

The Attempt at a Solution

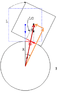
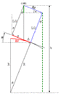
There is only one contact point between the cube and cylinder. There are three forces acting on the cube. The normal reaction from the cylinder, the friction and weight. The normal reaction and the friction pass through the contact point. Now how do I form the equations here?

Any help is appreciated. Thanks!

 

[voko]

It might be easier to find the potential energy due to gravity as a function of the block's tilt angle and then look for its minima.

 

[Saitama]

It might be easier to find the potential energy due to gravity as a function of the block's tilt angle and then look for its minima.

I calculate potential energy from the line passing through the centre of cylinder.

$$U(\theta)=mg\left(R+\frac{L}{2}\right)(1-\cos \theta)$$
where $\theta$ is the angle rotated by the cylinder.

The minima is at $\theta=0$ and for this $\theta$, $U''(\theta)>0$ but solving gives me a negative answer which is certainly incorrect.

 

[voko]

You seem to assume that the block will slide, so that its center of mass is on the line passing through center of the drum and the point of contact. But the block will roll over the drum, and the point of contact will shift.

 

[gneill]

Consider the following drawing:

Does that suggest an approach? Hint: Consider the difference between the displacement of the point of contact on the face of the block to where the vertical through the center of mass passes through the same face (the line segment named Δ on the enlargement of the right).

 

[Saitama]

Nice drawing gneill!

Is $\Delta=R\theta-(L/2)\tan\theta$?

How do I continue with voko's approach of finding potential energy? I need the distance of CM of cube from centre of cylinder but I don't see how to apply the geometry here.

 

[gneill]

Nice drawing gneill!

Is $\Delta=R\theta-(L/2)\tan\theta$?

Yes indeed. The answer should be obvious from that...

How do I continue with voko's approach of finding potential energy? I need the distance of CM of cube from centre of cylinder but I don't see how to apply the geometry here.

In my drawing, extend the radius on the right by L/2 making it a total of R + L/2 in length. Then draw a perpendicular line from its end to the center of mass position. Treat the two as vectors to locate the center of mass.

 

[Saitama]

Yes indeed. The answer should be obvious from that...

How?

Do I have to apply the condition that $\Delta \geq 0$?

In my drawing, extend the radius on the right by L/2 making it a total of R + L/2 in length. Then draw a perpendicular line from its end to the center of mass position. Treat the two as vectors to locate the center of mass.

Please look at the attachment. Are you talking about the vectors shown? I still don't see how can I find the distance of CM from them. :(

 

[gneill]

How?

Do I have to apply the condition that $\Delta \geq 0$?

That's the idea. Consider the direction of the torque provided by the weight of the block about its contact point. Under what conditions is it a restoring force? When is it going to make the angle of tilt increase? When will it be exactly neutral?

Please look at the attachment. Are you talking about the vectors shown? I still don't see how can I find the distance of CM from them. :(

You have the lengths of both, and they are perpendicular. You've even drawn in the hypotenuse!

 

[BruceW]

I Love these kinds of problems. Problems related to something that you might just be absent-mindedly thinking about, after trying to balance some cereal on a football. Pranav, you always bring nice problems :)

 

[WannabeNewton]

I Love these kinds of problems. Problems related to something that you might just be absent-mindedly thinking about, after trying to balance some cereal on a football. Pranav, you always bring nice problems :)

They're all from Kleppner and Kolenkow "An Introduction to Mechanics" (this particular one is from the chapter on rotational motion). Go get the book before I mail it to you myself!

 

[haruspex]

How?

Do I have to apply the condition that $\Delta \geq 0$?

Yes, bearing in mind that this is for arbitrarily small theta. You will need an approximation to get θ and tan θ comparable.

 

[BruceW]

They're all from Kleppner and Kolenkow "An Introduction to Mechanics" (this particular one is from the chapter on rotational motion). Go get the book before I mail it to you myself!

cool, I might check it out. It seems I've missed out on a real gem here :)

 

[haruspex]

There is an ambiguity in the question. The interpretation of 'stable' so far is (I think) that it doesn't tilt at all, but it could be read as not rolling right off (assuming adequate friction).

 

[gneill]

There is an ambiguity in the question. The interpretation of 'stable' so far is (I think) that it doesn't tilt at all, but it could be read as not rolling right off (assuming adequate friction).

I think the interpretation is that it's "stable" in the same sense that Lagrange Points are stable; A small perturbation induces a small orbit around the point rather than an escape trajectory.

So long as the cubical block is less than a certain size a small perturbation will result in oscillation rather than it tipping off of the cylinder. Larger than that critical size, any small perturbation will result in the angle increasing continuously -- i.e. falling off.

 

[haruspex]

I think the interpretation is that it's "stable" in the same sense that Lagrange Points are stable; A small perturbation induces a small orbit around the point rather than an escape trajectory.

So long as the cubical block is less than a certain size a small perturbation will result in oscillation rather than it tipping off of the cylinder. Larger than that critical size, any small perturbation will result in the angle increasing continuously -- i.e. falling off.

Yes, I agree, that's probably what's intended.
There's yet a third question one could ask: what's the largest L for which it is possible to place the block on the cylinder stably? What a rich source of puzzles.

 

[Saitama]

That's the idea. Consider the direction of the torque provided by the weight of the block about its contact point. Under what conditions is it a restoring force? When is it going to make the angle of tilt increase? When will it be exactly neutral?

Okay, I understand but looking over the sketch again, how did you find that angle between the perpendicular of length L/2 and vertical is $\theta$?

You have the lengths of both, and they are perpendicular. You've even drawn in the hypotenuse!

One of the lengths is R+L/2. I fail at determining the second side, Please help.

Just a guess, is it $R\theta$?

Pranav, you always bring nice problems :)

Thanks BruceW!

As WBN stated, some problems are from the book "Introduction to Mechanics by David Kleppner" and the other, which is much more interesting (sorry WBN, I prefer Irodov than Kleppner :P ) is this: https://www.amazon.com/dp/8183552153/?tag=pfamazon01-20

The above book is quite popular in India. You must check this and have a look at reviews on Amazon. :)

 

[gneill]

Okay, I understand but looking over the sketch again, how did you find that angle between the perpendicular of length L/2 and vertical is $\theta$?

There are numerous right-angles joining the line segments, so anything tilted will make angle θ with respect to either the horizontal or the vertical. The trick is to determine which (w.r.t. horizontal or vertical). Fortunately the shape of the triangles gives a big hint, but even so you could follow the trail of perpendicular lines from the tilted radius vector and label the angles w.r.t. horizontal and vertical as you go. I've added a few annotations to the diagram -- see the thumbnail.

One of the lengths is R+L/2. I fail at determining the second side, Please help.

Just a guess, is it $R\theta$?

Yes, it must be because the two L/2 length line segments are parallel and the line you want is parallel to the bottom of the cube. The resulting figure is a rectangle.

 

[voko]

Okay, I understand but looking over the sketch again, how did you find that angle between the perpendicular of length L/2 and vertical is $\theta$?

The cube is tangent to the drum at all times.

One of the lengths is R+L/2. I fail at determining the second side, Please help.

Just a guess, is it $R\theta$?

Your guess is right. Now try to explain it.

 

[Saitama]

There are numerous right-angles joining the line segments, so anything tilted will make angle θ with respect to either the horizontal or the vertical. The trick is to determine which (w.r.t. horizontal or vertical). Fortunately the shape of the triangles gives a big hint, but even so you could follow the trail of perpendicular lines from the tilted radius vector and label the angles w.r.t. horizontal and vertical as you go. I've added a few annotations to the diagram -- see the thumbnail.

Nicely explained, thanks gneill!

Since $\Delta \geq 0$ and $\theta$ is very small, $L\geq 2R$.

Yes, it must be because the two L/2 length line segments are parallel and the line you want is parallel to the bottom of the cube. The resulting figure is a rectangle.

Umm..I think I did not require it, I need the distance from the reference line to continue with the voko's approach. How do I find that?

What I get is $(L/2)/\cos(\theta)+\Delta \sin\theta+R-(x+\Delta \cos(\theta))$, is this correct?

 

[gneill]

Umm..I think I did not require it, I need the distance from the reference line to continue with the voko's approach. How do I find that?

What I get is $(L/2)/\cos(\theta)+\Delta \sin\theta+R-(x+\Delta \cos(\theta))$, is this correct?

Umm, distance of what from which reference line? Can indicate it on the diagram?

 

[Saitama]

Umm, distance of what from which reference line? Can indicate it on the diagram?

I have attached a picture.

 

[gneill]

The diagram shows a horizontal reference line through the center of the cylinder, but it doesn't indicate what distance you want. Is it the perpendicular distance of the center of mass of the block from that reference line?

 

[Saitama]

Is it the perpendicular distance of the center of mass of the block from that reference line?

Yes. :)

 

[gneill]

Okay, more diagram annotations. I draw your attention to the lines in green.

 

[Saitama]

This is what I get:

$$\frac{L}{2\cos\theta}+\Delta \sin\theta+R\cos\theta$$

Looks good?

 

[voko]

This might be easier in the vector language, which I think gneill suggested initially. Say the radius vector to the point of contact from the center is $\vec{r}(\theta)$. The unit vector corresponding to it is $\vec{u}(\theta)$. Then the extended radius vector is $(R + L/2) \vec u$. The tangential unit vector is $\vec t (\theta)$. So the position of CoM is $(R + L/2) \vec u - R \theta \vec t$. Then we only need the vertical component of the resultant vector to obtain the height.

 

[voko]

Oh, and $\vec t$ is obtained by differentiating $\vec u$.

 

[Saitama]

Then we only need the vertical component of the resultant vector to obtain the height.

And how do I find the vertical component?

 

[voko]

What are the components of $\vec u$?

 

[Saitama]

What are the components of $\vec u$?

$|\vec u| \sin\theta \hat{i}$ in horizontal and $|\vec u| \cos\theta \hat{j}$ in vertical? (where $\hat{i}$ and $\hat{j}$ are unit vectors in horizontal and vertical directions respectively)

 

[gneill]

This is what I get:

$$\frac{L}{2\cos\theta}+\Delta \sin\theta+R\cos\theta$$

Looks good?

You could do that, but it would be simpler to sum the two green line segments, both easily found.

 

[voko]

If you meant to say $\vec u = (\sin \theta, \cos \theta)$, yes. Pretty much by the unit circle trig definitions.

 

[Saitama]

You could do that, but it would be simpler to sum the two green line segments, both easily found.

Oops, you are right, it is simply $(R+L/2)\cos\theta + R\theta \sin \theta$. So the potential energy of block is $mg((R+L/2)\cos\theta + R\theta \sin \theta)$. Should I use the small angle approximation and then differentiate?

 

[gneill]

Oops, you are right, it is simply $(R+L/2)\cos\theta + R\theta \sin \theta$. So the potential energy of block is $mg((R+L/2)\cos\theta + R\theta \sin \theta)$. Should I use the small angle approximation and then differentiate?

Differentiate first. Isolate what you want to solve for, then apply any approximations required. You can also use limits.

 

[voko]

Is there any need to approximate anything? We just need to know the sign of the second derivative at $\theta = 0$.

 

[Saitama]

Differentiate first. Isolate what you want to solve for, then apply any approximations required. You can also use limits.

Let
$$U(\theta)=mg((R+L/2)\cos\theta+R\theta\sin\theta)$$
Differentiating wrt $\theta$
$$U'(\theta)=mg((R+L/2)(-\sin\theta)+R\sin\theta+R\theta\cos\theta)$$
Clearly, U(0)=0
$$U''(\theta)=mg((R+L/2)(-\cos\theta)+R\cos\theta+R\cos\theta-R\theta\sin\theta)$$

Since $U''(0)>0$,
$$-R-\frac{L}{2}+2R>0 \Rightarrow L>2R$$

Is this correct?

 

[voko]

Yes, that is correct. For an extra credit you could try and figure out what happens when $L = 2R$.

 

[Saitama]

Yes, that is correct. For an extra credit you could try and figure out what happens when $L = 2R$.

Many thanks voko & gneill!

I am not sure but I think it won't return to its initial position, it would stay in the same configuration. Right?

Also, does the block perform oscillatory or simple harmonic motion? Is it possible to find the time period of this motion?

 

[voko]

I am not sure but I think it won't return to its initial position, it would stay in the same configuration. Right?

That's only possible if the function were completely flat in some region around zero. Which is not the case here.

When examining extrema, vanishing of the second derivative is a special case, which requires examining higher order derivatives.

Also, does the block perform oscillatory or simple harmonic motion? Is it possible to find the time period of this motion?

Now that you have PE, you can write down conservation of energy and, using small-angle apprximations, get the SHM equation.

 

[Saitama]

When examining extrema, vanishing of the second derivative is a special case, which requires examining higher order derivatives.

I substituted $L=2R$. For this value of L, $U''(\theta)=-mgR\sin\theta \Rightarrow U'''(\theta)=-mgR\cos\theta$ For $\theta=0$, $U'''(0)=-mgR$. How do I interpret this?

Now that you have PE, you can write down conservation of energy and, using small-angle approximations, get the SHM equation.

After taking the approximations,
$$U(\theta)=mg\left(R+\frac{L}{2}+\frac{R\theta^2}{2}-\frac{L\theta^2}{4}\right)$$

At any instant of time, energy of block is
$$\frac{1}{2}I\omega^2+U(\theta)$$
where I is moment of inertia about CM and $\omega$ is angular velocity of block about CM, am I doing it right?

 

[voko]

I substituted $L=2R$. For this value of L, $U''(\theta)=-mgR\sin\theta$.

No. It is $-mg R \theta \sin \theta$.

How do I interpret this?

The principle is the same as with the second-order analysis. If the third derivative is not zero, that is not an extremum (why?). If it is, then everything depends on the sign of the fourth derivative, in exactly the same way (why?).

At any instant of time, energy of block is
$$\frac{1}{2}I\omega^2+U(\theta)$$
where I is moment of inertia about CM and $\omega$ is angular velocity of block about CM, am I doing it right?

Right, except that you want the moment with respect to the center of the drum, so that the block undergoes pure rotation.

 

[Saitama]

No. It is $-mg R \theta \sin \theta$.

Yes, very sorry. So $U'''(0)=-2mgR$.

The principle is the same as with the second-order analysis. If the third derivative is not zero, that is not an extremum (why?). If it is, then everything depends on the sign of the fourth derivative, in exactly the same way (why?).

From what I remember, if the third derivative is non-zero, then the point is an inflextion point. I don't understand how to interpret that in the given case.

Right, except that you want the moment with respect to the center of the drum, so that the block undergoes pure rotation.

voko, I don't know why but "pure rotation" about centre of drum does not make sense to me. I can't visualize how it is a pure rotation. The block tips to the right, comes back, tips left, comes back and the cycle goes on, how is it pure rotation about centre of drum? Sorry for asking so many dumb questions.

Differentiating the energy equation wrt time and setting the derivative to zero.

$$I\omega\alpha+U'(\theta)=0=I\omega\alpha+mg\left(\frac{R}{2}-\frac{L}{4}\right)(2\theta\omega)$$
$$\Rightarrow \alpha=\frac{mg}{I}\left(\frac{L}{2}-R\right)\theta$$

I don't think the above is correct, for SHM we must have $\alpha \propto -\theta$ but that doesn't seem to be the case here. :(

 

[voko]

Yes, very sorry. So $U'''(0)=-2mgR$.

No, still not correct. $U''(\theta) = -mg R \theta \sin \theta \to U'''(\theta ) = - mg R \sin \theta - mg R \theta \cos \theta \to U'''(0) = 0$

voko, I don't know why but "pure rotation" about centre of drum does not make sense to me. I can't visualize how it is a pure rotation. The block tips to the right, comes back, tips left, comes back and the cycle goes on, how is it pure rotation about centre of drum? Sorry for asking so many dumb questions.

Those are not dumb questions. The truth is, I was wrong and you are right doubting me. You could instead obtain the KE of CoM motion and the KE of block's rotation about CoM, just like you intended originally.

 

[Saitama]

No, still not correct. $U''(\theta) = -mg R \theta \sin \theta \to U'''(\theta ) = - mg R \sin \theta - mg R \theta \cos \theta \to U'''(0) = 0$

Very sorry again, I accidentally posted the value of the fourth derivative at $\theta=0$.

The fourth derivative is non-zero and negative, so do I say that equilibrium is stable in the case when $L=2R$?

Those are not dumb questions. The truth is, I was wrong and you are right doubting me. You could instead obtain the KE of CoM motion and the KE of block's rotation about CoM, just like you intended originally.

So the energy of block is
$$\frac{1}{2}mv^2+\frac{1}{2}I_{CM}\omega^2+U(\theta)$$

How do I relate v with $\omega$? Is $v=(L/\sqrt{2})\omega$?

 

[voko]

Very sorry again, I accidentally posted the value of the fourth derivative at $\theta=0$.

The fourth derivative is non-zero and negative, so do I say that equilibrium is stable in the case when $L=2R$?

The treatment of the fourth-order derivative is analogous to the second-order case, for largely the same reasons.

How do I relate v with $\omega$? Is $v=(L/\sqrt{2})\omega$?

You have already found the location of CoM in terms of the angle. Finding the velocity from that should be straight forward.

 

[Saitama]

You have already found the location of CoM in terms of the angle. Finding the velocity from that should be straight forward.

$$v_y=\frac{dh}{dt}$$

$$v_x=\frac{d}{dt}\left(\frac{L}{2}\sin\theta\right)$$

where $v_x$ is the horizontal velocity of block and $v_y$ is the vertical velocity of block.

I can replace $\omega$ with $d\theta/dt$.

Am I correct?

 

[voko]

What is $h$?

I was referring to the following formula of the CoM position: $(R + L/2) \vec u - R \theta \vec t$, where $\vec u$ is the unit radial vector, and $\vec t$ is the unit tangent vector, as explained earlier. The CoM velocity, then, is $v_c = (R + L/2) \dot {\vec u} - R \dot \theta \vec t - R \theta \dot {\vec t} = (R + L/2) \vec t \dot \theta - R \dot \theta \vec t + R \theta \vec u \dot \theta = (L/2) \vec t \dot \theta + R \theta \vec u \dot \theta$, and $v_c^2 = (L^2/4 + R^2 \theta^2) \dot \theta^2$

 

[Saitama]

What is $h$?

h is the height of CoM as shown in gneill's sketch in post #25.

I was referring to the following formula of the CoM position: $(R + L/2) \vec u - R \theta \vec t$, where $\vec u$ is the unit radial vector, and $\vec t$ is the unit tangent vector, as explained earlier. The CoM velocity, then, is $v_c = (R + L/2) \dot {\vec u} - R \dot \theta \vec t - R \theta \dot {\vec t} = (R + L/2) \vec t \dot \theta - R \dot \theta \vec t + R \theta \vec u \dot \theta = (L/2) \vec t \dot \theta + R \theta \vec u \dot \theta$, and $v_c^2 = (L^2/4 + R^2 \theta^2) \dot \theta^2$

I love the way you solve these problems using vectors. I wonder when I will get efficient in using them. :)

But I don't get the same answer as yours using my definition of $v_x$ and $v_y$.

Here's what I did:
$$v_x=\frac{L}{2}\dot{\theta}$$

Expression for h:
$$h=\left(R+\frac{L}{2}\right)\cos \theta+R\theta\sin\theta \approx \left(R+\frac{L}{2}\right)\left(1-\frac{\theta^2}{2}\right)+R\theta^2$$
Differentiating wrt time and simplifying, I get
$$v_y=\frac{dh}{dt}=\left(R-\frac{L}{2}\right)\theta\dot{\theta}$$
Also $v=\sqrt{v_y^2+v_x^2}$. But substituting the values doesn't give the same answer as yours. :(

 

[voko]

I suggest that you do the small angle approximation after you are done with finding the square of velocity. Then you will find the sine and cosine terms disappear and you do not have to approximate anything at all.

As for getting the hang of using vectors, you do that by using them :)