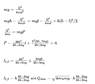Jorgen1224
- 36
- 0
I don't really know how to fit what i want to this template, but i'll try.
The thing is that i wonder if anyone can explain to me step-by-step what happened in this solution, because i don't really understand it.
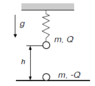
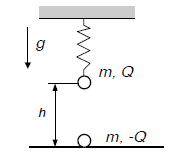
There are two balls. Upper one(mass m, charge Q) hung on a spring(coefficient k) is being held at the beggining and then it's dropped. Ball on the floor has mass m and charge -Q. Distance between them at the begginning is h.
What min. charge is required so that ball on the floor can jump.
Fe = k ⋅ q1 ⋅ q2 / r2
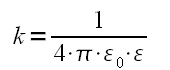
(There are two different k,one for spring and one from Coulomb's law. Sometimes i don't know which one is which)
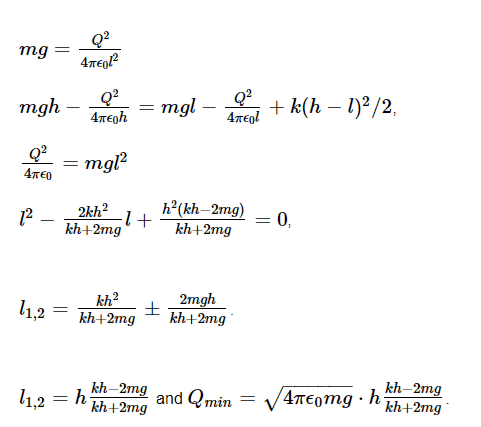
If i understood correctly l is min. distance between those two balls.
The thing is that i wonder if anyone can explain to me step-by-step what happened in this solution, because i don't really understand it.
Homework Statement
There are two balls. Upper one(mass m, charge Q) hung on a spring(coefficient k) is being held at the beggining and then it's dropped. Ball on the floor has mass m and charge -Q. Distance between them at the begginning is h.
What min. charge is required so that ball on the floor can jump.
Homework Equations
Fe = k ⋅ q1 ⋅ q2 / r2
(There are two different k,one for spring and one from Coulomb's law. Sometimes i don't know which one is which)
The Attempt at a Solution
If i understood correctly l is min. distance between those two balls.