Homework Help Overview
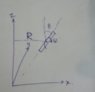
The problem involves a stick of length 2L and mass M that spins with angular velocity ω around an axis related to its center of mass (COM). The stick is positioned at an angle Θ with respect to the vertical axis, and there is an initial velocity v directed along the y-axis. The goal is to determine the precession radius R of the stick under these conditions.
Discussion Character
- Exploratory, Assumption checking, Conceptual clarification
Approaches and Questions Raised
- Participants discuss the torque τ and angular momentum L, with one participant attempting to relate these to gyroscopic motion. Others question the clarity of the problem statement, particularly regarding the axis of rotation and the physical setup of the stick. There is also a suggestion that the stick may be analogous to a spinning top precessing under gravitational influence.
Discussion Status
The discussion is ongoing, with participants seeking clarification on the initial problem statement and exploring the implications of the assumptions made. Some guidance has been offered regarding the need for a clearer depiction of the spin axis and the conditions under which the stick operates.
Contextual Notes
There are indications of potential errors in the problem statement, particularly concerning the treatment of forces acting on the stick, such as the aerodynamic lift coefficient and the neglect of gravity. The density of air is also mentioned, suggesting that fluid dynamics may play a role in the discussion.
