What is the pressure at point B in a moving liquid with density ρ?

  • Thread starter Thread starter Bestfrog
  • Start date Start date
  • Tags Tags
    Point Pressure
AI Thread Summary
The discussion centers on determining the pressure at point B in a moving liquid with density ρ. One participant references a solution stating that the pressure at B is p0 - ρg(h1 + d + h2), while another participant initially believes it should be p0 + ρg(-h1). The difference arises from the fluid's motion, which necessitates the application of Bernoulli's equation rather than static pressure calculations. The conversation emphasizes the importance of considering fluid dynamics in pressure calculations. Understanding these principles is crucial for accurately assessing pressure in moving fluids.
Bestfrog

Homework Statement


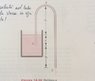
Considering the figure. The liquid has a density $$\rho$$. What is the pressure at B?
HHMiWcU

http://imgur.com/HHMiWcU
(I put the link because the image uploaded doesn't work)

The Attempt at a Solution


In a solution that I have found on internet, it is said that the pressure in B is $$p_0 - \rho g (h_1 + d+h_2 )$$. How is it possible? I thought that the pressure at B was $$p_0 + \rho g (-h_1)$$
 
Last edited by a moderator:
Physics news on Phys.org
I post the photo
 

Attachments

  • IMG_0223.JPG
    IMG_0223.JPG
    28.5 KB · Views: 422
Bestfrog said:
? I thought that the pressure at B was $$p_0 + \rho g (-h_1)$$
That would be true in a static arrangement, but the fluid is moving. Try Bernoulli's equation.
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

How to calculate the velocity of water streaming into the boat?
Replies
19
Views
949
Gauge pressure due to a floating body
Replies
4
Views
2K
What helium mass in a balloon to make it bouyant in air?
Replies
12
Views
1K
What is the issue with calculating the gauge pressure of object B?
Replies
1
Views
3K
Chimney effect and pressure difference
Replies
10
Views
2K
Bouyant force when there is no liquid beneath an object
Replies
8
Views
2K
Pressure on the wall of aquarium
Replies
7
Views
3K
Clarifying the Definition Total/Stagnation Pressure (p₀) in Bernoulli'
Replies
2
Views
887
What are the variables that affect the pressure of a gas in a capillary tube?
Replies
3
Views
2K
Calculating Pressure & Density Proportions with Changing Altitude & Temperature
Replies
19
Views
2K

Hot Threads

Recent Insights

Back
Top