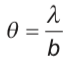youmei0426
- 18
- 0
Homework Statement
question (iii)
2. Homework Equations
D=sd/λ (where D is the distance from slit to screen, s is the distance to the central maxima, and d is the slit separation)[/B]
The Attempt at a Solution
I plugged the values s=0.3*10^(-3), d=4.5*10^(-3) and λ=633*10^(-9), and got the answer 2.13m. However, the answer stays that I need to multiply this value by 2, and I don't know why as the formula doesn't say so. Thanks in advance![/B]