uchicago2012
- 74
- 0
Homework Statement
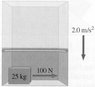
In the figure, a 25 kg block is pulled by a 100 N force and slides across the floor of the elevator. The coefficient of friction is µ = 0.35. If the elevator is accelerating downward at 2.0 m/s2, what is the resulting acceleration of the block?
See Figure 1
Homework Equations
F = u * Fn
where F = friction force, u = coefficient of friction force and Fn = normal force
Fnet = ma
where m= mass and a = acceleration
The Attempt at a Solution
So I decided the three forces acting on the block are Fn (normal force), Fg (force due to gravity), and F (horizontal force). I can find Fn of the block relatively easily, but I'm not sure what to assign the force Fg as. I don't think that it's as simple as Fg = mg because the block is not in free fall. Can I say Fg is 2.0 m/s2 * 25 kg? Then I would theoretically have all of the forces acting on the block and would be able to solve the equation Fnet = ma for a. I find this idea unsettling however, since I think that means the block would be slammed into the ceiling of elevator during this descent, since the downward force Fg is only 50 N and the upward force Fn is about 286 N.
Also, since the block is moving in two dimensions, this means I should solve for ax and ay separately, correct? So when I give my answer should I give it in Cartesian coordinates like a= 5 xhat + 8 xhat or should I convert it to magnitude angle notation? I didn't know if there was a standard preference.