bulldog23
- 120
- 0
[SOLVED] Conservation of Momentum
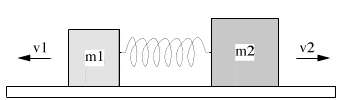
Two blocks with masses m1 = 2.6 kg and m2 = 3.6 kg are at rest on a frictionless surface with a compressed spring between them. The spring is initially compressed by 60.0 cm and has negligible mass. When both blocks are released simultaneously and the spring has dropped to the surface, m1 is found to have a speed of 3.0 m/s. What is the speed of m2?
P=m*v
I am trying to figure out the initial momentum of the system, so do I m1v1=m2v2?
Homework Statement
Two blocks with masses m1 = 2.6 kg and m2 = 3.6 kg are at rest on a frictionless surface with a compressed spring between them. The spring is initially compressed by 60.0 cm and has negligible mass. When both blocks are released simultaneously and the spring has dropped to the surface, m1 is found to have a speed of 3.0 m/s. What is the speed of m2?
Homework Equations
P=m*v
The Attempt at a Solution
I am trying to figure out the initial momentum of the system, so do I m1v1=m2v2?