What is the tension in a pulley system with multiple weights?

In summary, the system is in equilibrium with weightless and frictionless pulleys and weights of 25 N, 4 N, 4 N, and 1 N. Using the equation F=ma and considering each pulley and mass in a free body diagram, the tension T can be found by first finding the tension in the three strings and then drawing an FBD for each mass. The 25N weight has three forces acting on it: its own weight, the tension of the rope at the bottom, and the tension of the rope at the top.
  • #1
JeyGamer
2
0

Homework Statement


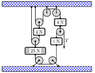
The system is in equilibrium and the pulleys are weightless and frictionless. The weights are 25 N, 4 N, 4 N, and 1 N. Find the tension T. The acceleration of gravity is 9.8 m/s^2. Answer in units of N


Homework Equations


F=ma


The Attempt at a Solution


Honestly, we've never done with a pulley system with multiple weights in class, so I don't know how to begin. I also don't know how to address the fact that some pulleys are connected to the center of another pulley.
 

Attachments

  • pulley.png
    pulley.png
    6.7 KB · Views: 699
Physics news on Phys.org
  • #2
You need to consider each pulley and each mass in a FBD. It is not difficult, but may be a bit tedious.
 
  • #3
Okay, but what do I do in a FBD for the 25N weight, which is connected to the center of a pulley?
 
  • #4
To make the problem easier first try to find the Tension in the 3 strings. And then as Voko said draw FBD of each mass. I don't think you need to make FBD of pulleys.
 
  • #5
JeyGamer said:
Okay, but what do I do in a FBD for the 25N weight, which is connected to the center of a pulley?

The 25N weight has three forces: its own weight, the tension of the rope at the bottom, and the tension of the rope at the top. Just like any other weight, really.
 

1. How does a pulley with multiple weights work?

A pulley with multiple weights works by distributing the load of the weights evenly across the pulley system. This allows for easier lifting of heavy objects as the weight is distributed among multiple ropes and pulleys.

2. What are the benefits of using a pulley with multiple weights?

The main benefit of using a pulley with multiple weights is that it reduces the amount of force needed to lift heavy objects. This makes it easier for a single person to lift heavy loads and also reduces the risk of injury.

3. How many weights can a pulley with multiple weights handle?

The number of weights that a pulley with multiple weights can handle depends on the strength and design of the pulley system. However, in general, a pulley with multiple weights can handle several hundred pounds of weight.

4. What is the difference between a fixed and a movable pulley in a pulley system with multiple weights?

A fixed pulley is attached to a stationary object and does not move, while a movable pulley is attached to the object being lifted and moves with it. In a pulley system with multiple weights, a combination of fixed and movable pulleys is used to distribute the weight and make lifting easier.

5. How can I calculate the mechanical advantage of a pulley with multiple weights?

The mechanical advantage of a pulley with multiple weights can be calculated by dividing the weight of the object being lifted by the amount of force needed to lift it. The more pulleys and ropes used in the system, the higher the mechanical advantage and the easier it is to lift the weight.

Similar threads

System of two pulleys and three masses
    • Introductory Physics Homework Help
Replies
22
Views
3K
Force applied on the pulley of a system
    • Introductory Physics Homework Help
Replies
8
Views
2K
Finding the period of pulley system
    • Introductory Physics Homework Help
Replies
22
Views
2K
Experimental Design: Pulley and Mass Hangers
    • Introductory Physics Homework Help
Replies
30
Views
1K
Acceleration due to *equal* weights on pulley system
    • Introductory Physics Homework Help
Replies
22
Views
4K
Defining equilibrium and movement in pulley arrangements
    • Introductory Physics Homework Help
Replies
8
Views
1K
Which forces am I missing in the FBDs?
    • Introductory Physics Homework Help
Replies
9
Views
1K
Explain friction in a pulley system
    • Introductory Physics Homework Help
Replies
13
Views
5K
What are the accelerations in the multiple-pulley problem?
    • Introductory Physics Homework Help
Replies
10
Views
2K
Torque of Pulley with Two Masses2
    • Introductory Physics Homework Help
Replies
6
Views
1K

Hot Threads

Recent Insights

Back
Top