What is the terminal velocity of an aluminum loop in a magnetic field?

[JohnDuck]

Homework Statement

Verbatim from the book:
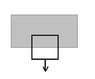
A square loop is cut out of a thick sheet of aluminum. It is then placed so that the top portion is in a uniform magnetic field B, and allowed to fall under gravity. (In the diagram, shading indicates the field region; B points into the page.) If the magnetic field is 1 Tesla, find the terminal velocity of the loop (in m/s). Find the velocity of the loop as a function of time. How long does it take (in seconds) to reach, say, 90% of the terminal velocity? What would happen if you cut a tiny slit in the ring, breaking the circuit?

I've attached a reproduction of the diagram.

Homework Equations

Lorentz force law (perhaps?):
F = q(E + B x v)

The Attempt at a Solution

I'm completely stumped, not even sure where to start. It doesn't make sense to talk about terminal velocity unless there's some force resisting the motion of the loop. However, as far as I can tell, there is none. The loop will simply drop out of the field region, and subsequently only experience a force due to gravity (i.e., no terminal velocity).

http://img233.imageshack.us/img233/7659/diagramna2.jpg

 

[Hootenanny]

HINT: Consider the induced current in the loop

 

[JohnDuck]

Sorry, could you elaborate on that? It's not clear to me how to calculate the induced current, considering the dimensions of the loop are not given.

 

[Hootenanny]

Sorry, could you elaborate on that? It's not clear to me how to calculate the induced current, considering the dimensions of the loop are not given.

Ahh, but you know that the loop is a square so it's area is $\ell^2$ where $\ell$ is the length of one side. Furthermore,

$$A = \ell^2 \Rightarrow \frac{dA}{dt} = 2\ell\cdot\frac{d\ell}{dt}$$

But,

$$\frac{d\ell}{dt} = v$$

Hence,

$$\frac{dA}{dt} = 2\ell\cdot v}$$

Do you follow?

Edit: A decent reference: http://hyperphysics.phy-astr.gsu.edu/Hbase/electric/elevol.html#c3