- #1
Femme_physics
Gold Member
- 2,550
- 1
Wiki says:
Isn't this exactly what every A/D converter does?
For a graph of Vin to digital output it basically approximates the nearest digital value to the continuous signal ->
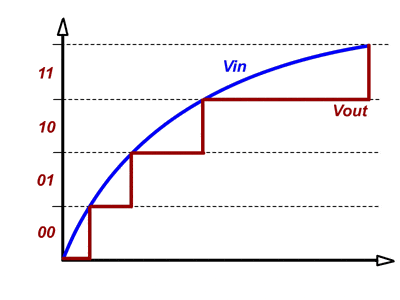
So I don't see the difference between them.
A successive approximation ADC is a type of analog-to-digital converter that converts a continuous analog waveform into a discrete digital representation via a binary search through all possible quantization levels before finally converging upon a digital output for each conversion.
Isn't this exactly what every A/D converter does?
For a graph of Vin to digital output it basically approximates the nearest digital value to the continuous signal ->
So I don't see the difference between them.