What's the point of a voltmeter having a high internal resistance?

[needingtoknow]

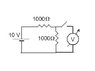
Homework Statement

I understand that voltmeters are supposed to have high internal resistances so that they won't draw much current. However, they are being attached parallel to the resistor anyways and according to Kirchhoff' Law that means the voltage through both the resistor for which we are trying to measure the voltage and for the voltmeter, they will both experience the same voltage. Why does the voltmeter need to have a high internal resistance then. Isn't it redundant or unnecessary according to Kirchhoff law.

 

[Orodruin]

The voltmeter is connected parallel to a component of the circuit. This means the resistance (or impedance) of that part of the circuit is going to change, which in general changes the potential drop across the component. This effect will be larger if the voltmeter has lower resistance (to the point of completely ignoring the component if the voltmeter resistance goes to zero).

Thus, in order to get an accurate measure of what the potential would be without the voltmeter, it needs to have a high resistance.

 

[needingtoknow]

That makes sense because charge always takes the path of least resistance, so the charge might move through the voltmeter path if it wasn't so high. I agree with your explanation.

But how does that tie into Kirchoff's Law about the voltage being constant for every branch that are in parallel?

 

[phinds]

But how does that tie into Kirchoff's Law about the voltage being constant for every branch that are in parallel?

You are ignoring the effect of the rest of the circuit.

If you have an ideal voltage source hooked directly across a resistor, and you use a voltmeter to measure the voltage, then it doesn't matter what the internal resistance of the voltmeter is. But of course it that case you are, in a real sense, not even measuring the voltage across the resistor so much as you are measuring the voltage across the source. If you were to remove the resistor, it would have no effect on the voltage.

 

[ehild]

See the attached picture. You wan to measure the voltage across the vertical resistor. The internal resistance of the voltmeter is also 1000Ω.

The "real" voltage is 5 V, but connecting the voltmeter parallel with the resistor, you get 500 Ω resistance connected in series with the horizontal resistor. The net resistance of the circuit is 1500Ω, and the current drawn from the battery is I=10/1500 A. The voltage across the parallel connected resistor and voltmeter is 500I=10/3=3.3 V. The voltmeter changed the voltage you wanted to measure.
If the internal resistance of the voltmeter is much higher, 1 MΩ for example, connecting parallel with 1000 Ω would results in 999 Ω, net resistance would be 1999 Ω, and the voltmeter would measure (10/1999)999=4.997V. You see the error is much less.

ehild

 

[AlephZero]

But how does that tie into Kirchoff's Law about the voltage being constant for every branch that are in parallel?

When you use the voltmeter, you are adding another component to the circuit (i.e. a resistor equal to the internal resistance of the meter).

Kirchoff's Laws only apply to one circuit at a time. If you change the circuit, KVL and KCL give you a different set of equations, with a different solution. The reason for making the voltmeter resistance large is because you want the two sets of equations have nearly the same solutions.

In some situations, even with a high resistance voltmeter you have to make a correction to the meter reading, because the circuit you are measuring (including the meter) is not the same as the circuit you want to study.

 

[CWatters]

Only modern voltmeters have a high resistance. In my dads day most voltmeters were made by yourself using a moving coil meter and resistors to change the scaled. The resistance of the voltmeter was frequently low enough to have an effect on the circuit it was being used to measure. You had to get used to taking this into account. As AlephZero said...you still do in some circumstances.

 

[sophiecentaur]

That makes sense because charge always takes the path of least resistance, so the charge might move through the voltmeter path if it wasn't so high. I agree with your explanation.

But how does that tie into Kirchoff's Law about the voltage being constant for every branch that are in parallel?

Owch! That is just not true and it'ss a huge oversimplification. The charge flow (current) is shared, according to the resistances in each leg, and it it really wrong to say it all goes one way.
The higher the resistance of the voltmeter, the smaller share of the current and the less it will influence the measurement.

 

[Okefenokee]

It actually ties into Thevenin's theorem.

Thevenin's theorem states that you can pick any two points of a network of resistors and sources and reduce them to a single source and a single resistor in series. That's called a Thevenin equivalent circuit and it is a virtual model of the real circuit. If you measure the voltage across any two points and the meter's impedance is low compared to that virtual resistance then the voltage will be lower at the meter than it is at the source by the voltage divider rule. Now your measurement will have a dependence on the impedance of the meter.

A more simple way to explain it would be to say that a really high resistance will not disturb a circuit. If you have, for example, a 100 GigaOhm resistor you could plug it into any real device in the world and pretty much nothing would happen don't you think? The resistance is so high that it is practically an open circuit.

An ideal voltage meter should have infinite resistance. What do you suppose the resistance of an ideal Ammeter should be?

 

[sophiecentaur]

This is where Engineering comes in. No measuring instrument is 'good enough'; they all have their limits and we learn to work round them. We do all our measurements with boxing gloves and rubber rulers, even though we may not recognise it.

 

[Vanadium 50]

Only modern voltmeters have a high resistance.

What is your definition of modern? VTVM's were in common use in the 1950's and had an internal resistance in the 10's of megohms. (11 was a very popular value) The circuit was patented in 1916.

 

[mrspeedybob]

Besides all the other observations made here, volt meters are not only used for scientific experiments, but also as diagnostic tools. If I want to know why a circuit is not functioning as intended I need to find out what the circuit is actually doing. If my volt meter drew a current which was significant in the scheme of the circuit I was testing then I would change the operation of the circuit by connecting the meter, this would make it much more difficult to diagnose.

This is why diagnostics on modern automobiles are done mainly with volt meters instead of test lights as was the case years ago.

 

[Sturk200]

I guess this question is kind of old, but I have an explanation that might be helpful to someone.

Consider a circuit that consists of two resistors in series. We wish to measure the voltage across one of them, say R1, and so attach a voltmeter across it. The voltmeter acts as a resistor (say with resistance Rv) and therefore when we place it in parallel with R1 it will create an equivalent resistance of (R1)(Rv)/R1+Rv. Now in order for the voltage across this element of the circuit to change minimally upon the introduction of the voltmeter (and note that the voltage will change since we are dealing with two resistors in series), we want the new equivalent resistance to be as close to R1 as possible. By observing the expression for the equivalent resistance, we see that this is the case when Rv is much greater than R1, for then (R1)(Rv)/[Rv(1+(R1/Rv))] = (R1)(Rv)/Rv = R1. (Since R1/Rv goes to zero).

So really the requirement that a voltmeter have a high resistance is a consequence of the way in which resistances are added when placed in parallel.

 

[phinds]

So really the requirement that a voltmeter have a high resistance is a consequence of the way in which resistances are added when placed in parallel.

Your explanation is a good one, but the "resistances are added when place in parallel" is very misleading. They DON'T "add".

 

[sophiecentaur]

Your explanation is a good one, but the "resistances are added when place in parallel" is very misleading. They DON'T "add".

Yes. It is the Conductances (1/R) that add. Hence the Parallel Resistance formula.