jfierro
- 20
- 1
This is from Sadiku's Elements of electromagnetics. I have come to a result but it's different from that of the book.
Three identical small spheres of mass m are suspended by threads of negligible
masses and equal length l from a common point. A charge Q is divided equally
between the spheres and they come to equilibrium at the corners of a horizontal equilateral
triangle whose sides are d. Show that
Q^2 = 12\pi\epsilon_0mgd^3 \begin{bmatrix} l^2 - \frac{d^2}{3}\end{bmatrix}^{-\frac{1}{2}}
F = \frac{q_1q_2}{4\pi\epsilon_0R^2}\mathbf{a_r}
This is all given by the book.
The way I see this problem is as follows:
http://img256.imageshack.us/img256/6063/sadikuex4.png
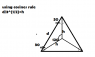
P being the common point, Fe being the force exerted by the other 2 speheres, mg being the force exerted by gravity.
The equilateral triangle would be the top view, while the right triangle is a side view of one of the spheres.
The length of w in the right triangle is:
d\sqrt{3}
from the inscribed circle formula in an equilateral triangle.
If we define alpha as the P angle on the right-angle triangle, and T as the tension on each thread caused by both the electrostatic force and weight of a sphere, then:
T\sin \alpha = F_e
T\cos \alpha = mg
\frac{\sin \alpha}{\cos \alpha} = \frac{F_e}{mg} (1)
But, by the superposition principle:
F_e = \frac{1}{4\pi\epsilon_0} \frac{q^2}{d^2} + \frac{1}{4\pi\epsilon_0} \frac{q^2}{d^2} = \frac{1}{2\pi\epsilon_0} \frac{q^2}{d^2} (2)
where
q = \frac{Q}{3} (3)
is the charge of an individual sphere.
Now,
\tan \alpha = \frac{w}{h}
h = \frac{w}{\tan \alpha}
l^2 = \frac{w^2}{\tan^2 \alpha} + w^2 = \frac{3d^2}{\tan^2 \alpha} + 3d^2
\tan^2 \alpha = \frac{3d^2}{l^2 - 3d^2}
\tan \alpha = \sqrt{3}d( l^2 - 3d^2 )^{-\frac{1}{2}} (4)
Substituting (2), (3) and (4) in (1) and solving for Q yields:
Q^2 = 18\sqrt{3}\pi\epsilon_0mgd^3( l^2 - 3d^2 )^{-\frac{1}{2}}
What's wrong?
Thanks and best regards.
Homework Statement
Three identical small spheres of mass m are suspended by threads of negligible
masses and equal length l from a common point. A charge Q is divided equally
between the spheres and they come to equilibrium at the corners of a horizontal equilateral
triangle whose sides are d. Show that
Q^2 = 12\pi\epsilon_0mgd^3 \begin{bmatrix} l^2 - \frac{d^2}{3}\end{bmatrix}^{-\frac{1}{2}}
Homework Equations
F = \frac{q_1q_2}{4\pi\epsilon_0R^2}\mathbf{a_r}
This is all given by the book.
The Attempt at a Solution
The way I see this problem is as follows:
http://img256.imageshack.us/img256/6063/sadikuex4.png
P being the common point, Fe being the force exerted by the other 2 speheres, mg being the force exerted by gravity.
The equilateral triangle would be the top view, while the right triangle is a side view of one of the spheres.
The length of w in the right triangle is:
d\sqrt{3}
from the inscribed circle formula in an equilateral triangle.
If we define alpha as the P angle on the right-angle triangle, and T as the tension on each thread caused by both the electrostatic force and weight of a sphere, then:
T\sin \alpha = F_e
T\cos \alpha = mg
\frac{\sin \alpha}{\cos \alpha} = \frac{F_e}{mg} (1)
But, by the superposition principle:
F_e = \frac{1}{4\pi\epsilon_0} \frac{q^2}{d^2} + \frac{1}{4\pi\epsilon_0} \frac{q^2}{d^2} = \frac{1}{2\pi\epsilon_0} \frac{q^2}{d^2} (2)
where
q = \frac{Q}{3} (3)
is the charge of an individual sphere.
Now,
\tan \alpha = \frac{w}{h}
h = \frac{w}{\tan \alpha}
l^2 = \frac{w^2}{\tan^2 \alpha} + w^2 = \frac{3d^2}{\tan^2 \alpha} + 3d^2
\tan^2 \alpha = \frac{3d^2}{l^2 - 3d^2}
\tan \alpha = \sqrt{3}d( l^2 - 3d^2 )^{-\frac{1}{2}} (4)
Substituting (2), (3) and (4) in (1) and solving for Q yields:
Q^2 = 18\sqrt{3}\pi\epsilon_0mgd^3( l^2 - 3d^2 )^{-\frac{1}{2}}
What's wrong?
Thanks and best regards.
Last edited by a moderator: