bagasme
- 79
- 9
Hello,
In high school, I had been taught about finding substitution resistance from Wheatstone bridge.
The formula:
a. If the cross product of ##R1## and ##R3## is same as ##R2## and ##R4##, the galvanometer in the middle (##R_5##) can be omitted and use series-parallel principle to solve for the substitution resistance.
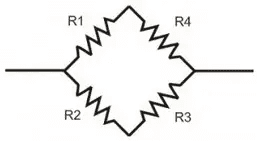
b. If instead the cross products are different, modify the circuit to the following diagram below,
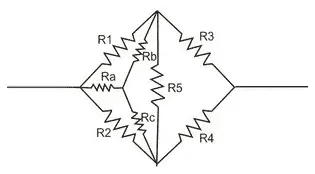
and determine new resistances (##R_a##, ##R_b##, & ##R_c##) by:
$$\begin{align}
R_a &= \frac {R_1 \cdot R_2} {R_1 + R_2 + R_5} \nonumber \\
R_b &= \frac {R_1 \cdot R_5} {R_1 + R_2 + R_5} \nonumber \\
R_c &= \frac {R_2 \cdot R_5} {R_1 + R_2 + R_5} \nonumber
\end{align}$$
Then, use new resistance to solve for substitution resistance.
However, there isn't any explanation or derivation of the formula AFAIK (even on my textbook).
So what derivation that lead me to the formulas above?
Bagas
In high school, I had been taught about finding substitution resistance from Wheatstone bridge.
The formula:
a. If the cross product of ##R1## and ##R3## is same as ##R2## and ##R4##, the galvanometer in the middle (##R_5##) can be omitted and use series-parallel principle to solve for the substitution resistance.
b. If instead the cross products are different, modify the circuit to the following diagram below,
and determine new resistances (##R_a##, ##R_b##, & ##R_c##) by:
$$\begin{align}
R_a &= \frac {R_1 \cdot R_2} {R_1 + R_2 + R_5} \nonumber \\
R_b &= \frac {R_1 \cdot R_5} {R_1 + R_2 + R_5} \nonumber \\
R_c &= \frac {R_2 \cdot R_5} {R_1 + R_2 + R_5} \nonumber
\end{align}$$
Then, use new resistance to solve for substitution resistance.
However, there isn't any explanation or derivation of the formula AFAIK (even on my textbook).
So what derivation that lead me to the formulas above?
Bagas