When exactly does error -> zero in calculus-based mechanics?

[EddiePhys]

I've come across many instances where sometimes the error tends to zero but other times it does not. Let me give you a few examples.

1.
When I calculate the volunme of a sphere summing up discs of height dy from -R to +R, the error in volume tends to zero as Delta y->0 but when I'm calculating the surface area using rings of height dy, this error does not tend to zero.
Same with a hollow cone vs a solid cone.

2.

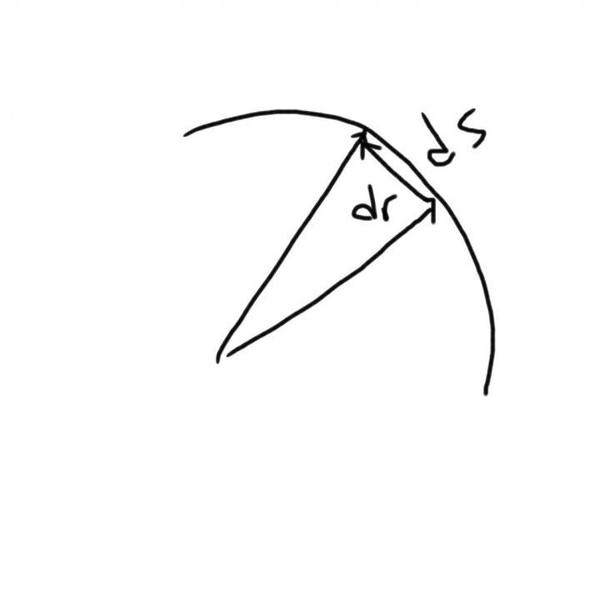
ds is the arc length. We know ds/dt = speed = |dr/dt| since the error tends to zero.

However, in another case, particularly from Irodov's problems:

3.
I'm trying to find the work done by the spring as the block moves from one end to the other(Yes' I'm aware there are easier ways of going about it)

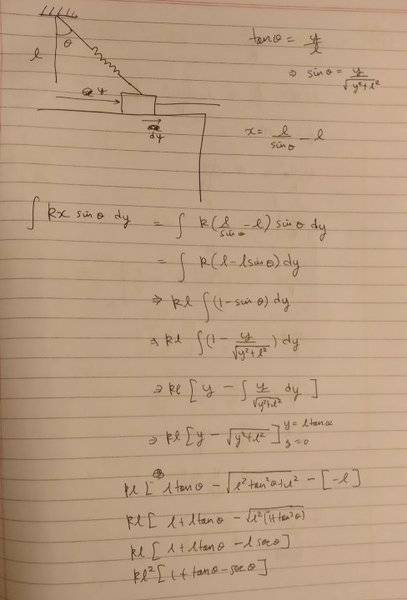
Here, where I think I'm going wrong is assuming the spring force to be constant in the interval dy when it can only remain constant during an infinitesimal displacement along the spring.

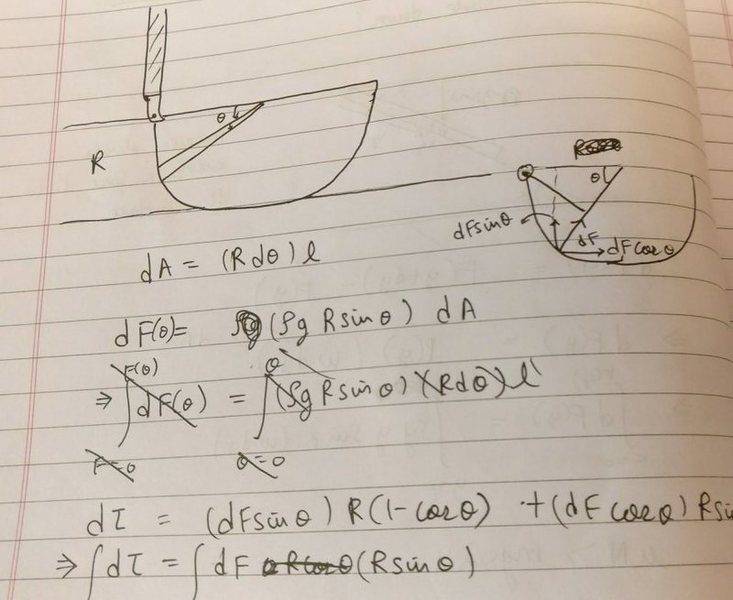
However, here we assume pressure to be constant in the interval Rdtheta when it really only is constant in the interval dH since it's a function of h

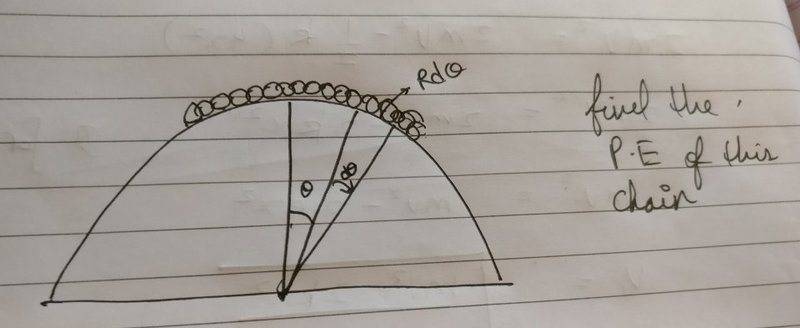
And here, we assume the potential energy of the chain to be constant in the interval Rdtheta when it should be only constant in dh yet in these two cases the error tends to zero but it doesn't in the first case.

 

[BvU]

A lot of questions. Post as separate threads. For now: number 1 looks like an error in the calculation. Can you show post it ?

 

[EddiePhys]

This doesn't seem to be getting any replies. Have I posted in the wrong subsection?

 

[fresh_42]

This doesn't seem to be getting any replies. Have I posted in the wrong subsection?

Well, as I see it, it may be better placed in the homework section and one question per thread. (And don't forget to use the template.) I understand that the photos are helpful for your drawings, but usually people don't appreciate handwriting very much. So maybe you could type it in LaTeX instead, and use photos only if really needed.

 

[Khashishi]

For calculating surface area, or similarly the arc length, you need to find an infinitesimal shape that approximates the slope of the surface, not just the position.
Consider a simple diagonal line from (0,1) to (1,0). It has length $\sqrt(2)$. If you approximate it as a staircase, and take the stair height ->0, then you get something that looks like the diagonal line. It matches the position of the diagonal line, so it gives you the correct area under the curve. But it gives you an arc length of 2. It is because you have not matched the slope anywhere. The approximate curve has a slope of 0 and infinity alternating infinitely often, whereas the original curve has a slope of -1.

 

[BvU]

This doesn't seem to be getting any replies. Have I posted in the wrong subsection?

Strange. On my screen I do see a reply. It's called post #2 and it asks you to elaborate on your statement:

when I'm calculating the surface area using rings of height dy, this error does not tend to zero

where I suspect it will be rather easy to point out your mistake

 

[EddiePhys]

For calculating surface area, or similarly the arc length, you need to find an infinitesimal shape that approximates the slope of the surface, not just the position.
Consider a simple diagonal line from (0,1) to (1,0). It has length $\sqrt(2)$. If you approximate it as a staircase, and take the stair height ->0, then you get something that looks like the diagonal line. It matches the position of the diagonal line, so it gives you the correct area under the curve. But it gives you an arc length of 2. It is because you have not matched the slope anywhere. The approximate curve has a slope of 0 and infinity alternating infinitely often, whereas the original curve has a slope of -1.

Thanks a lot! :D Could you also please answer the other questions?