- #1
abhishek4
- 12
- 0
In thermodynamics when can we say that ΔH = ΔU?
Well, for cases where ##\Delta(PV)=0##abhishek4 said:In thermodynamics when can we say that ΔH = ΔU?
That is true but when I asked my teacher she also said that in a closed system this is possible. Why is that?Chestermiller said:Well, for cases where ##\Delta(PV)=0##
Do you think that delta PV can't be zero in a closed system? What about a process involving an ideal gas for which there is vo temperature change?abhishek4 said:That is true but when I asked my teacher she also said that in a closed system this is possible. Why is that?
I know that in a closed system there is no change in volume and we can assume that pressure is remaining constant too but then using the ideal gas equation moles come out to be constant too so in such a case moles formed must be equal to the moles reacted which does not happen in all cases. I just wanted to know if someone could give me an example of this so that i could understand it better. An example of an equation would help.Chestermiller said:Do you think that delta PV can't be zero in a closed system? What about a process involving an ideal gas for which there is vo temperature change?
You never mentioned that you were exclusively talking about situations involving chemical reaction. Is that what you want to focus on?abhishek4 said:I know that in a closed system there is no change in volume and we can assume that pressure is remaining constant too but then using the ideal gas equation moles come out to be constant too so in such a case moles formed must be equal to the moles reacted which does not happen in all cases. I just wanted to know if someone could give me an example of this so that i could understand it better. An example of an equation would help.
Yes, i am sorry i forgot to mention that in the post.Chestermiller said:You never mentioned that you were exclusively talking about situations involving chemical reaction. Is that what you want to focus on?
If it is a reaction involving ideal gases, then it happens if the number of moles of products is equal to the number of moles of reactants (stoichiometrically).abhishek4 said:Yes, i am sorry i forgot to mention that in the post.
There is no flow work in a close system ΔPV=0, since ΔH=ΔU+ΔPV. The gas can not expand, so what happens is, internal energy of the gas can be measured by simply the difference in its temperature→ CvΔTabhishek4 said:That is true but when I asked my teacher she also said that in a closed system this is possible. Why is that?
Are you really saying that Δ(PV) = 0 for any process in a closed system?Ronie Bayron said:There is no flow work in a close system ΔPV=0, since ΔH=ΔU+ΔPV.
Are you really saying that, when a chemical reaction occurs in a closed system, the change in internal energy is CvΔT?The gas can not expand, so what happens is, internal energy of the gas could be measured by simply the difference in its temperature→ CvΔT
Yes, Chester. Why? Is there something wrong with it?Chestermiller said:Are you really saying that Δ(PV) = 0 for any process in a closed system?
Yes Chester, could there by any more energy unaccounted by it?Chestermiller said:Are you really saying that, when a chemical reaction occurs in a closed system, the change in internal energy is CvΔT?
Hi Ronie,Ronie Bayron said:Yes, Chester. Why? Is there something wrong with it?
Yes Chester, could there by any more energy unaccounted by it?
How and why? I am delighted and loved to see the reasons why its bordering misinformation. Isn't that suppose the goal of the forum, to educate people in the right track. I have no problem getting wronged, when it's proven.Chestermiller said:Hi Ronie,
Actually neither of your answers is correct. I was just checking to see if you really meant what you seemed to indicate. Your answers come very close to bordering on misinformation, which is a no-no at Physics Forums. Please, in the future, if your expertise is not sufficient to address a member's questions, do not offer answers. All this does is confuse the member further. Understand that misinformation can lead to infraction points and eventual banning.
Chet
My problem is not with your desire to learn in Physics Forums, but with the authoritative manner in which you gave your answer in post #9 (considering it was incorrect), and your lack of qualifying statements for what you were saying.Ronie Bayron said:How and why? I am delighted and loved to see the reasons why its bordering misinformation. Isn't that suppose the goal of the forum, to educate people in the right track. I have no problem getting wronged, when it's proven.
Here is my reference analysis for "bomb calorimeter" from Ohlone College.
Chestermiller said:My problem is not with your desire to learn in Physics Forums, but with the authoritative manner in which you gave your answer in post #9 (considering it was incorrect), and your lack of qualifying statements for what you were saying.
Chestermiller said:With regard to your response in the first statement, Δ(PV) is not generally equal to zero even in an isolated system, let alone in a closed system. If the volume is constant in a closed system, then Δ(PV)= VΔP, and if the pressure is constant in a closed system, then Δ(PV)=PΔV. And then there are all those other cases in which both P and V change in a closed system.
Chestermiller said:Now for the second statement you agreed to: when a chemical reaction occurs in a closed system, the change in internal energy is CvΔT. Now, we're not talking about the calorimeter here (which contains the reacting system), we are talking about the actual set of chemical species that constitute the reaction mixture. You are aware that, even if the temperature and pressure of a system are unchanged between the initial and final states of the system, its internal energy and enthalpy can still change, correct?
I assume you have heard of changes in phase which occur at constant temperature and pressure? Examples are melting and vaporization. You are aware that both the enthalpy and internal energy of the material change during a phase change at constant temperature and pressure? You have heard of the terms heat of vaporization and heat of melting, correct? So, for these, the internal energy change is not equal to CvΔT.
Chestermiller said:In the case of chemical reactions, there are energy effects associated with making and breaking of chemical bonds. You are aware that both the enthalpy and the internal energy of the reacting mixture change during a chemical reaction at constant temperature and pressure (or constant temperature and volume)? You have heard of the terms heat of reaction, heat of combustion, and heat of formation, correct? So, for these, the internal energy change is not equal to CvΔT.
Further questions?
Who says that, in an isochoric process, ΔH=ΔU? For an isochoric process ΔH=ΔU+VΔP.Ronie Bayron said:I am sorry Chet, we seemed to have a disconnect here.
In post #9, I was responding to OP's query "In thermodynamics when can we say that ΔH = ΔU?". To cut the chase, my answer was direct to the point. CvΔT(sensible heat) refers to an Isochoric process.
ΔH is not equal to ΔU unless Δ(PV)=0.You caught me like a lawyer on that one, for the term "close" system, probably, lost the case. Isothermal & Isobaric expansion also happens in a close system, I agree, but it's far from the point of ΔH = ΔU which is in the first place the, OP's concern.
Yes I do have a good understanding of it. You would not need to determine the values of specific heat in the lab for heat of reaction, heat of combustion, and heat of formation, because these changes are defined at constant temperature. They represent the amount of heat (per mole) that must be added to the system to hold it at constant temperature in going from pure reactants to pure products.Nope and yes, one more. Then, how would you measure or determine the values of specific heat in the lab for "heat of reaction, heat of combustion, and heat of formation"? I suppose you have a good understanding on this.
So, the analysis of below source is erroneous or probably lack some consideration of VdP? How would that differ with ΔH=ΔU?Chestermiller said:Who says that, in an isochoric process, ΔH=ΔU? For an isochoric process ΔH=ΔU+VΔP.
Then, when is Δ(PV)=0? Is this condition hypothetical?Chestermiller said:ΔH is not equal to ΔU unless Δ(PV)=0.
Chestermiller said:Yes I do have a good understanding of it. You would not need to determine the values of specific heat in the lab for heat of reaction, heat of combustion, and heat of formation, because these changes are defined at constant temperature. They represent the amount of heat (per mole) that must be added to the system to hold it at constant temperature in going from pure reactants to pure products.
This derivation is correct. But I don't see any ΔH in there. So, what makes you think that this proved ΔH=ΔU? Here's what I get by continuing this analysis: $$ΔH=ΔU+Δ(PV)=nC_vΔT+nRΔT=n(C_v+R)ΔT=nC_pΔT$$Ronie Bayron said:So, the analysis of below source is erroneous or probably lack some consideration of VdP? How would that differ with ΔH=ΔU? View attachment 95979
No. For an ideal gas, it is when ΔT=0Then, when is Δ(PV)=0? Is this condition hypothetical?
No way. The equation you wrote applies to an ideal gas mixture at CONSTANT TEMPERATURE. So, for a pure ideal gas (or a non-reacting ideal gas mixture), even though Δn=0, if the temperature changes, ΔH≠ΔU. For that case, as we showed above, ##ΔU=nC_vΔT## and ##ΔH=nC_pΔT##, you are referring to that (T) temperature right? Generally, for medium involving chemical reaction, right? Consequently, for pure substance that does not undergo chemical reaction the change of number of moles Δn is zero. So, the term becomes zero for pure substance, right? Therefore, analysis for pure substance simplifies into ΔH=ΔU. Do you agree on this?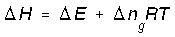
Yes, but only at constant temperature.But, for medium which undergoes chemical reaction, Δn≠0 therefore, ΔH=ΔE+ΔngRT, is this correct?
Obviously not.Thus, we can summarize ΔH for isochoric process as follows
For (Pure Substance - does not undergo chemical reaction) ----> ΔH=ΔU
For (Substance that undergoes chemical reaction)------------------> ΔH=ΔE+ΔngRT
Do you agree on this?
So, what's the difference of ΔH, ΔU & Q in this set-up.? How do you define ΔH then?Chestermiller said:This derivation is correct. But I don't see any ΔH in there. So, what makes you think that this proved ΔH=ΔU?
Chestermiller said:Here's what I get by continuing this analysis: $$ΔH=ΔU+Δ(PV)=nC_vΔT+nRΔT=n(C_v+R)ΔT=nC_pΔT$$
Do you have a problem with this.
How can a gas mixture has Δn? Mixture does not react, so Δn=0 and of course ΔH= ΔE only .Chestermiller said:No way. The equation you wrote applies to an ideal gas mixture at CONSTANT TEMPERATURE.
You're saying you have a degree in Mechanical Engineering, and you don't know how ΔH is defined, correct? H = U + PV, and ΔH = ΔU + Δ(PV). In this setup, ΔH=ΔU+VΔP=ΔU+nRΔTRonie Bayron said:So, what's the difference of ΔH, ΔU & Q in this set-up.? How do you define ΔH then?
View attachment 96008
I see that you have an issue, but I don't know what that issue is.No, I don't have the problem with that derived equation but, how it's used, I have an issue.
How can a gas mixture has Δn? Mixture does not react, so Δn=0 and of course ΔH= ΔE only .
No. Your problem is much more fundamental than this. You just haven't learned thermodynamics properly.I just do not know, I can not somehow agree with you. May be because we are from different field.
Enthalpy is defined in all thermo textbooks as H ≡ U + PV. For an open flow system operating at steady state like the type you are describing, the change in enthalpy of the flowing stream is not equal to the sum of the change in internal energy plus the flow work (sometimes called shaft work). For an incompressible fluid passing between entrance and exit of a system like that, the rate of change of enthalpy for the flowing stream is equal to ##\dot{m}\Delta h= \dot {m} (\Delta u+v\Delta P)##, where ##\dot{m}## is the mass flow rate, and the lower case letters represent properties per unit mass. Check your textbook and see.Enthalpy for me is a equation of a state basing on the First Law of Thermodynamics which is "arbitrarily" set to sum up(internal energy+flow work)at a point, so if there is no flow work done, enthalpy ΔH reduces to internal energy ΔU. That's is what the book said, the way we are taught and we use to run boilers and steam engines.
Oh yeah? What if I told you that, if you check your steam tables, you will find that the specific internal energy values u differ from the specific enthalpy values h by the product of the specific volume times the pressure vP? That is h = u + pV. What do you think about that? So even your own steam tables back up what I have been saying.Otherwise if yours is true-that for a closed system at constant volume( ΔH=ΔU+VΔP) , we will have to revised a new steam tables, probably.
No, you said that. I know what I am doing.Chestermiller said:You're saying you have a degree in Mechanical Engineering, and you don't know how ΔH is defined, correct? H = U + PV, and ΔH = ΔU + Δ(PV). In this setup, ΔH=ΔU+VΔP=ΔU+nRΔT
Needless to say, I know that. So you now see where VΔP is applicable(incompressible fluids), yes? Try steam on a turbine if it follows the same formula ##\dot{m}\Delta h= \dot {m} (\Delta u+v\Delta P)##Chestermiller said:Enthalpy is defined in all thermo textbooks as H ≡ U + PV. For an open flow system operating at steady state like the type you are describing, the change in enthalpy of the flowing stream is not equal to the sum of the change in internal energy plus the flow work (sometimes called shaft work). For an incompressible fluid passing between entrance and exit of a system like that, the rate of change of enthalpy for the flowing stream is equal to ##\dot{m}\Delta h= \dot {m} (\Delta u+v\Delta P)##, where ##\dot{m}## is the mass flow rate, and the lower case letters represent properties per unit mass. Check your textbook and see.
So, how do we connect ΔH=ΔU +VΔP in there for a constant volume analysis?Chestermiller said:Oh yeah? What if I told you that, if you check your steam tables, you will find that the specific internal energy values u differ from the specific enthalpy values h by the product of the specific volume times the pressure vP? That is h = u + pV. What do you think about that? So even you own steam tables back up what I have been saying.
Hi Chet, sweet!Chestermiller said:So Ronie,
When do you want to start working on that focus problem? I was hoping you would be up to the challenge.
Chet
OK. Fasten your seat belt.Ronie Bayron said:Hi Chet, sweet!I had a reply on this, posted couple of months ago, but it was gone. I wonder why. Anyhow, yes Chet, go ahead.

Yes according to spiraxsarco.com container should have volume of 1.69612 m3per kg of steam and all the rest are given on the attached table of values.Chestermiller said:OK. Fasten your seat belt.
I have 1kg of superheated water vapor at 1 bar and 100 C in a closed rigid container. This is going to be the initial condition. From your steam tables, what is the volume of the container? What is the specific volume of the water vapor, the specific internal energy, and specific enthalpy?
Chet
Good. The two steam table references I have both give H = 2676.2 kJ/kg. So we are pretty much in agreement on that. But I asked you to provide the internal energy U from your steam tables under these conditions, and there is no value given in your table. So what is the value from your source? We can't continue until you provide this.Ronie Bayron said:Yes according to spiraxsarco.com container should have volume of 1.69612 m3per kg of steam and all the rest are given on the attached table of values.
Yes, let us use this, perhaps.Chestermiller said:Good. The two steam table references I have both give H = 2676.2 kJ/kg. So we are pretty much in agreement on that. But I asked you to provide the internal energy U from your steam tables under these conditions, and there is no value given in your table. So what is the value from your source? We can't continue until you provide this.
Chet
Excellent! That summarizes the initial state of our system. Now, to get to our final state, we are going to gradually add heat to the 1 kg of vapor in our rigid container until its pressure is 1.5 bars. From your steam tables, what is the final temperature, volume, internal energy, and enthalpy of our vapor?Ronie Bayron said:Yes, let us use this, perhaps.
@ 1 bar, 100 deg C
v = 1.6959 m3/kg
u = 2506.2 kJ/kg
h = 2675.8 kJ/kg
Let us just make it 1.6 bars to avoid numerous interpolation since its readily available on the table. Again, we recall initial stateChestermiller said:Excellent! That summarizes the initial state of our system. Now, to get to our final state, we are going to gradually add heat to the 1 kg of vapor in our rigid container until its pressure is 1.5 bars. From your steam tables, what is the final temperature, volume, internal energy, and enthalpy of our vapor?
Chet
I asked for the results at 1.5 bar, and that's what I want. Also, if the mass of water vapor is 1 kg, and the volume of the rigid container hasn't changed, then has the specific volume of the vapor changed between the initial and final states? Also, regarding your statement that "given process does not lost heat," what did you think I meant when I said "we are going to gradually add heat to the 1 kg of vapor in our rigid container?"Ronie Bayron said:Let us just make it 1.6 bars to avoid numerous interpolation since its readily available on the table. Again, we recall initial state
@ initial state 1 bar, 1000C (we'll include entropy)
v = 1.6959 m3/kg
u = 2506.2 kJ/kg
h = 2675.8 kJ/kg
s = 7.3611 kJ/kg-K
@ Final State 1.6 bar, (s = 7.3611 kJ/kg-K) given process does not lost heat, ideally.
Values of T is in between 4000C and 5000C
View attachment 98056
O you're so fast. Haven't got enough time to think and edit my post.Chestermiller said:I asked for the results at 1.5 bar, and that's what I want. Also, if the mass of water vapor is 1 kg, and the volume of the rigid container hasn't changed, then has the specific volume of the vapor changed between the initial and final states? Also, regarding your statement that "given process does not lost heat," what did you think I meant when I said "we are going to gradually add heat to the 1 kg of vapor in our rigid container?"
Chet
It's not so essential to prove your point. Let's just cut the chase. Is that okay with you?Chestermiller said:I asked for the results at 1.5 bar, and that's what I want
Well, we said we were going to do it strictly by using your steam tables (to make sure I'm not trying to pull a fast one). Later, we can compare with the ideal gas law, but, for now I'd like to stick with the steam tables. Besides, if you assume an ideal gas, you still will have to deal with the problem of determining the internal energy and the enthalpy at the final state.Ronie Bayron said:O you're so fast. Haven't got enough time to think and edit my post.
Anyhow, isentropic process was mistake to describe what you want.- since you add up heat gradually and heat is not by some sort of chemical potential, inside a perfect adiabatic enclosure in which case can also be true at conditions you describe.
I realized, that this is isochoric process. It can not be found on the table fixated @ final v = 1.6959 m3/kg which remains as is, no matter what. Assuming water vapor behaves an ideal gas above regions of the saturated vapor curve, we can find T using PV =mRT or T = PV/mR; where R- is specific gas constant of water of course. This holds true unless, you rebutted.
Do you have problem with this?It's not so essential to prove your point. Let's just cut the chase, okay with you?
Do you have any to recommend? So what's the value of u and h @ 1.5 bars & v = 1.6959 m3/kgChestermiller said:Well, we said we were going to do it strictly by using your steam tables (to make sure I'm not trying to pull a fast one). Later, we can compare with the ideal gas law, but, for now I'd like to stick with the steam tables. Besides, if you assume an ideal gas, you still will have to deal with the problem of determining the internal energy and the enthalpy at the final state.
There are steam tables online that have the properties evaluated at 1.5 bar, if you want to avoid that interpolation (and I deliberately chose 1.5 bar because one of the specific volume values listed in the table at 1.5 bar is almost exactly our specific volume, so you wouldn't have to do any interpolating). However, if you can't find a steam table with 1.5 bar in it, I will settle for your using 1.6 bar. But then you will have to interpolate with respect to the specific volume to get the temperature, internal energy and enthalpy. Your choice.
I got one by googling "steam tables," but it was a PDF file, and I don't know how to get the actual URL. There are also steam tables in thermo books I have (that are consistent with the PDF table). In Moran et al, they give v = 1.695 m^3 at 280 C, with u = 2778.6 kJ/kg and h = 3032.8 kJ/kg. If you are comfortable using these values, we can continue.Ronie Bayron said:Do you have any to recommend? So what's the value of u and h @ 1.5 bars & v = 1.6959 m3/kg