- #1
Gauss177
- 38
- 0
1. A 160 cm tall person lies on a light (massless) board which is supported by two scales, one under the feet and one beneath the top of the head. The scale under the feet reads 29.4 kg and the one under the head reads 32.8 kg. Where is the center of gravity of this person measured from the bottom of the feet?
My thoughts:
The person would feel 321.4 N (32.8 kg * 9.8) pushing up at the head, and 288.1 N (29.4 kg * 9.8) pushing up at the feet. The force of mg would be an arrow pointing down under the center of gravity, located x meters from the bottom of the feet. For person to be in equilibrium, Fnet must equal 0, so:
321.4 N + 288.1 N = F
F = 609.6 N
Also, torque must also equal 0, so:
321.44(1.6) = 609.56(x)
x = .844 m, or 84.4 cm from the bottom of the feet.
Is this correct?
------------------
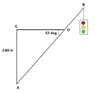
2. A traffic light hangs from a structure as shown in the attached picture. The uniform aluminum pole AB is 4.5 m long and weighs 5.0 kg. The weight of the traffic light is 10.0 kg. Determine the tension in the horizontal massless cable CD, and the vertical and horizontal components of the force exerted by the pivot A on the aluminum pole.
My thoughts:
I drew a free body diagram of the aluminum pole AB, and made the point A as my "fulcrum." Then, I would only have to worry about mg of the pole (5*9.8=49 N), Mg of the light (10*9.8=98 N), and tension T exerted by the cable CD. I split T into its components, Tx and Ty, and since Fnet must equal 0 for it to be at equilibrium:
Ty = 49 + 98 = 147 N
Therefore, Tx = 147 tan 37 = 110.72 N
I'm really not sure how to do the second part: finding the vertical and horizontal components of the force exerted by the pivot on the pole. I'm probably not visualizing it correctly, so please help.
My thoughts:
The person would feel 321.4 N (32.8 kg * 9.8) pushing up at the head, and 288.1 N (29.4 kg * 9.8) pushing up at the feet. The force of mg would be an arrow pointing down under the center of gravity, located x meters from the bottom of the feet. For person to be in equilibrium, Fnet must equal 0, so:
321.4 N + 288.1 N = F
F = 609.6 N
Also, torque must also equal 0, so:
321.44(1.6) = 609.56(x)
x = .844 m, or 84.4 cm from the bottom of the feet.
Is this correct?
------------------
2. A traffic light hangs from a structure as shown in the attached picture. The uniform aluminum pole AB is 4.5 m long and weighs 5.0 kg. The weight of the traffic light is 10.0 kg. Determine the tension in the horizontal massless cable CD, and the vertical and horizontal components of the force exerted by the pivot A on the aluminum pole.
My thoughts:
I drew a free body diagram of the aluminum pole AB, and made the point A as my "fulcrum." Then, I would only have to worry about mg of the pole (5*9.8=49 N), Mg of the light (10*9.8=98 N), and tension T exerted by the cable CD. I split T into its components, Tx and Ty, and since Fnet must equal 0 for it to be at equilibrium:
Ty = 49 + 98 = 147 N
Therefore, Tx = 147 tan 37 = 110.72 N
I'm really not sure how to do the second part: finding the vertical and horizontal components of the force exerted by the pivot on the pole. I'm probably not visualizing it correctly, so please help.
Attachments
Last edited: