- #1
AntigenX
- 77
- 0
Simple question (derived from some unanswered posts from various posters, mostly mitesh9)...
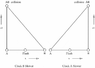
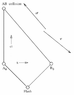
Two identical clocks A (stationary) and B (moving towards A) with a relative velocity v, so that it will collide with A after some time. (the notion of stationary/moving is for the sake of simplicity, otherwise, its impossible to judge it as per SR)
The clocks are set to read "zero" by a flesh of light equidistant from both. That means, they are set to the origin of their time axis. their spetial co-ordinates are different but their time co-ordinates at the start (flash of light) are same, which can be used as a reference to calculate their respective accumulated time, to which both the clocks will agree.
The clocks are of special kind, and have some mechanism that is infinitely sensitive to touch. so the clocks will stop the moment they are touched by the other clock. Note that, acceleration has no part to play, because, the clocks stop before the acceleration starts.
Now the questions.
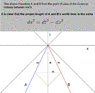
1. When they collide, the clocks will stop. Which clock has accumulated less time? Presumably B, but how, because, we can not tell which clock is moving/stationary.
2. For clocks to collide, they should have same spacetime co-ordinates. Though their space co-ordinates are same at the time of collision, their time co-ordinates will be different (due to time dilation sufferred by B), in which case, they should not collide at all? How can they collide then? And if they do, then where has gone the time dilation?
3. More questions If the discussion proceeds ...
...
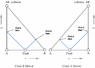
Two identical clocks A (stationary) and B (moving towards A) with a relative velocity v, so that it will collide with A after some time. (the notion of stationary/moving is for the sake of simplicity, otherwise, its impossible to judge it as per SR)
The clocks are set to read "zero" by a flesh of light equidistant from both. That means, they are set to the origin of their time axis. their spetial co-ordinates are different but their time co-ordinates at the start (flash of light) are same, which can be used as a reference to calculate their respective accumulated time, to which both the clocks will agree.
The clocks are of special kind, and have some mechanism that is infinitely sensitive to touch. so the clocks will stop the moment they are touched by the other clock. Note that, acceleration has no part to play, because, the clocks stop before the acceleration starts.
Now the questions.
1. When they collide, the clocks will stop. Which clock has accumulated less time? Presumably B, but how, because, we can not tell which clock is moving/stationary.
2. For clocks to collide, they should have same spacetime co-ordinates. Though their space co-ordinates are same at the time of collision, their time co-ordinates will be different (due to time dilation sufferred by B), in which case, they should not collide at all? How can they collide then? And if they do, then where has gone the time dilation?
3. More questions If the discussion proceeds