Which cube has a larger moment of inertia?

[Cosmossos]

To which of the two cubes has a larger moment of inertia?

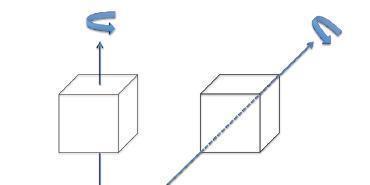
I think it's the right one because We know that the minimal moment of inertia is throw the principal axes that goes throw the center of mass. in the right one , the rotation isn't throw the principal axes . there is also the following theorem :

The moment of inertia about an arbitrary axis is equal to the
moment of inertia about a parallel axis passing through the
center of mass plus the moment of inertia of the body about
the arbitrary axis, taken as if all of the mass M of the body
were at the center of mass.

Am I wrong?

 

[diazona]

If I'm reading your diagram correctly, the parallel axis theorem wouldn't apply since in both cases, the axis passes through the center of mass of the cube. But if the moment of inertia is always minimized around a principal axis, that would be a valid reason for arguing that the one on the right is greater.

Personally, I might try to work it out by integration to really convince myself.