Which of these spring systems is equivalent?

[MarkH748]

Hi guys. I looking at a vibrations problem with 2 springs in it (System A). I need to find an overall value for the stiffness K to find the natural frequency of the system. I know that normally when 2 springs are in series I should get the sum of (I/Ki)^-1 which would give me an equivilant stiffness of K/2 in this case (System C). But when I take moments about the pivot point og the rod O it makes more sense to me for it to be 2K (System B). Here are some sketches I made.

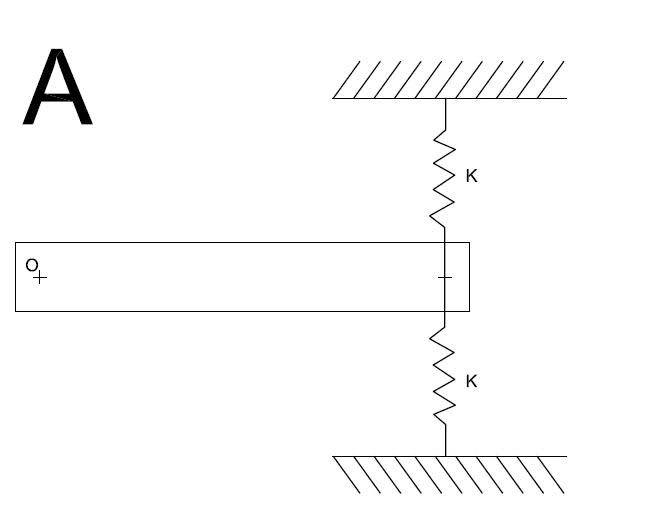
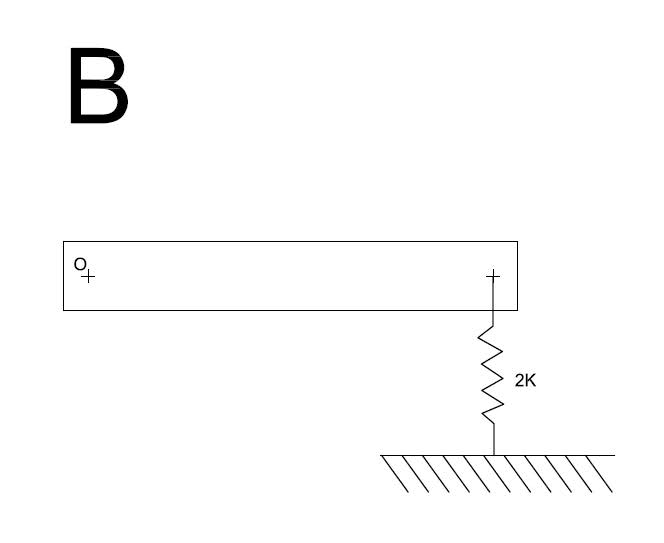
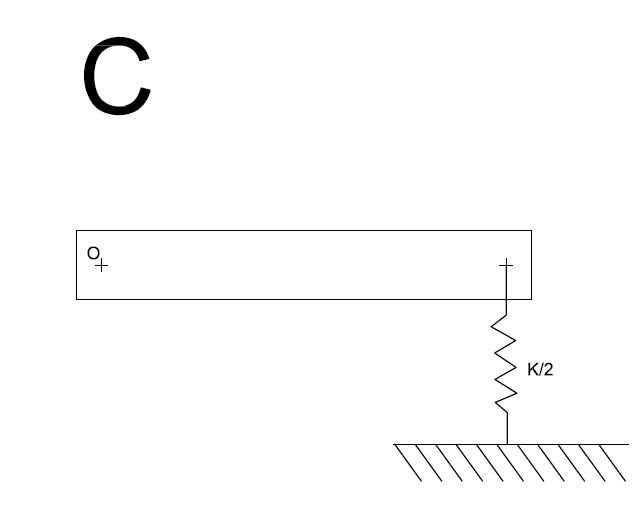
Can anyone shed some light on this as I'm unsure of which system is correct.

Any help would be greatly appreciated.

Mark.

 

[Doc Al]

I know that normally when 2 springs are in series I should get the sum of (I/Ki)^-1 which would give me an equivilant stiffness of K/2 in this case (System C).

Ah... but you don't really have two springs in series, you have one above and one below. Why not derive the effective spring constant for yourself? (Imagine the rod displaced by some Δx. What's the net force on it?)