Kyle Nemeth
- 25
- 2
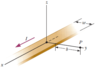
We are asked to find the magnetic field at point P, all of the quantities in the figure are known values and the current density is uniform. One way to solve this problem is by modeling the sheet as a collection of infinitely long wires, with each wire contributing an amount of magnetic field dB and then integrating to find the total magnetic field. Why is it that this approach must be used and not an approach involving Ampere's Law directly?