Why Cherenkov light leave rings instead of full circles?

[A.R.]

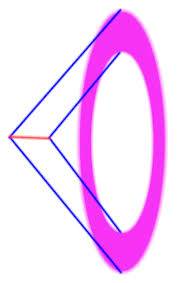
If the image we obtain from Cherenkov light is actually the projection of a continuous wave front (Fig. 1) on a vertical plane, orthogonal respect to the direction of propagation of the incident particle, why we just see a ring (Fig. 2), instead of a full circle? Is it because Cherenkov light is produced only during a brief period, between the entrance of the incident particle in the radiator medium and the instant when its velocity drops below the threshold (Fig. 3)?

Fig. 1

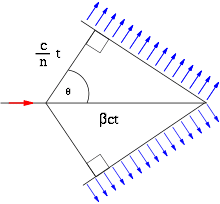
Fig. 2

Fig. 3

 

[ChrisVer]

What is the difference between a ring and a full-circle?
To me fig.2 looks pretty much as a full-circle...however you can find its fluctuation around the circle by trying a fit and looking at the point differences...However that would be too crude, because your events are of course pixels and not points, and your machine (itself) has some offset signals (the points which are very far away from the circle)

 

[A.R.]

Do you know how light/particle detectors work?
Fig. 2 is a ring, because only border detectors are activated, while inner detectors are off as well as outer ones. I'm asking, if the wave front is continuous, from the axis of the cone, to the maximum radius of the projection, why the image is not a full ring? I.e., why Fig. 2 is not a full orange circle? My answer is Fig. 3, where the red segment is the path the particle makes between the entrance in the medium and the drop of its velocity under the threshold for Cherenkov production, with the stop of light production and introduction of the discontinuity. But, is it really in this way?

 

[mfb]

There are two options:

(1) the one you mentioned, a short slab of material where the radiation is emitted and then a long distance to the detector.
(2) (curved) mirrors that reflect all light emitted in a specific direction to the same position

Both are used.

 

[A.R.]

There are two options:

(1) the one you mentioned, a short slab of material where the radiation is emitted and then a long distance to the detector.
(2) (curved) mirrors that reflect all light emitted in a specific direction to the same position

Both are used.

So, if the detector is in contact with the material, the particle radiates until it reaches the detector, and the detector is just a plain sheet of PMs, what we'll see is actually a full circle, right?

 

[mfb]

It would be a filled circle (a disk), yes.