drop_out_kid
- 34
- 2
- Homework Statement
- verify the uncertainty principle by wave function of infinite well free particle(ground state)
- Relevant Equations
- \sai(x)=\sqrt {2/L} sin(Pi*x/L)dx
So I think I use the right approach and I get uncertainty like this:
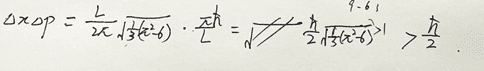
And it's interval irrelevant(ofc),
So what kind of wave function gives us \h_bar / 2 ? I guess a normal curve? if so, why is normal curve could be? if not then what's kind of wave function can reach the lower bound
And it's interval irrelevant(ofc),
So what kind of wave function gives us \h_bar / 2 ? I guess a normal curve? if so, why is normal curve could be? if not then what's kind of wave function can reach the lower bound