Why Does an Inductor Behave Differently from a Resistor in an RL Circuit?

[hopkinmn]

Homework Statement

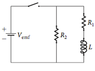
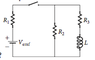
I'm having trouble understanding how RL circuits work. Here's my understanding so far. Let me know where I'm going wrong. I've provided a reference image.

Right after the switch is closed, the current through R1 and R2 is zero. The potential difference for these two resistors is also zero. The inductor has a current . The potential difference across the inductor is equal to Vemf.

But why is it that the current through R2 is zero, but there is current through the inductor?Shouldn't they be the same since they are in series?

Homework Equations

V=IR

 

[gneill]

Inductors appear as open circuits to abrupt changes in potential, not short circuits. It's capacitors that look like short circuits under those circumstances.

So... for the instant after the switch is closed, erase L from the circuit and then analyze!

 

[hopkinmn]

So then as time goes to infinity, does the current through the inductor go to zero?

 

[hopkinmn]

Also, for this different circuit, suppose the switch has been closed for a long time and then reopened. Upon reopening, the currents through the three resistors would be V/Rx, where x is 1, 2, or 3.
After the switch has been opened for a long time, does the inductor act as the battery for the right side? So that I1=0, but I2=I3=some value?

 

[gneill]

So then as time goes to infinity, does the current through the inductor go to zero?

No, as time goes to infinity the inductor behaves like a short circuit.

 

[gneill]

Also, for this different circuit, suppose the switch has been closed for a long time and then reopened. Upon reopening, the currents through the three resistors would be V/Rx, where x is 1, 2, or 3.

No, when the switch opens R1 is no longer in a closed circuit; there's nowhere for current to flow. Current through the other resistors will depend upon the energy stored in the inductor -- inductor current does not "want" to change immediately, so its current must take whatever paths are available to it when the switch opens.

After the switch has been opened for a long time, does the inductor act as the battery for the right side? So that I1=0, but I2=I3=some value?

You haven't indicated what i1, i2, or i3 are, so it's difficult to comment...
But for the given circuit with the switch open, with no constant supply of power to the right hand side of the circuit, any energy stored in the inductor must eventually be lost as power is dissipated by the resistors as current flows.

 

[Quantus]

If I wanted to calculate the Inductor's equivalent resistance at a given time after the circuit closes, how would I do that?

This is how inductors act as filters, correct? By allowing slow pulses but resisting the rate of change required by fast pulses?

 

[gneill]

If I wanted to calculate the Inductor's equivalent resistance at a given time after the circuit closes, how would I do that?

Determine the current through and potential across the inductor for a given time. Equivalent resistance is the Potential/Current.

This is how inductors act as filters, correct? By allowing slow pulses but resisting the rate of change required by fast pulses?

More or less, yes. Inductors resist quick changes in current (sort of a "current inertia").