Minhtran1092
- 28
- 2
I'm trying to figure out a way to fasten a [book] shelf onto a wall without using corbels. I decided to use L-brackets for support but I positioned them horizontally instead of vertically.
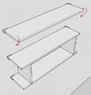
In the attached image, there are two designs:
1. A single shelf fastened to drywall using two drywall anchors, each rated for 70-lb.
2. Two shelves, as described above, screwed together using two boards stood on their edges. The two vertical boards are not fastened to the wall.
When attached to the wall and under no load, design 1 rotates forward under its own weight.
Design two, despite being fastened to the wall the same way as design 1, could hold at least 70kg (I did not find its failing point - I hung my weight off of it).
Despite being fastened to the wall the same way, why did the wall-shelf connection in design 1 fail with no load while design 2 was able to support much more?
In the attached image, there are two designs:
1. A single shelf fastened to drywall using two drywall anchors, each rated for 70-lb.
2. Two shelves, as described above, screwed together using two boards stood on their edges. The two vertical boards are not fastened to the wall.
When attached to the wall and under no load, design 1 rotates forward under its own weight.
Design two, despite being fastened to the wall the same way as design 1, could hold at least 70kg (I did not find its failing point - I hung my weight off of it).
Despite being fastened to the wall the same way, why did the wall-shelf connection in design 1 fail with no load while design 2 was able to support much more?