SmokeyBear
- 2
- 0
When a male bighorn sheep runs head-first into another male, the rate at which its speed drops to zero is dramatic. Figure 9-11 gives a typical graph of the acceleration a versus time t for such a collision, with the acceleration taken as negative to correspond to an initially positive velocity. The peak acceleration has magnitude 34 m/s2 and the duration of the collision is 0.27 s. Assume that the sheep's mass is 90.0 kg. What are the magnitudes of the impulse and average force due to the collision?
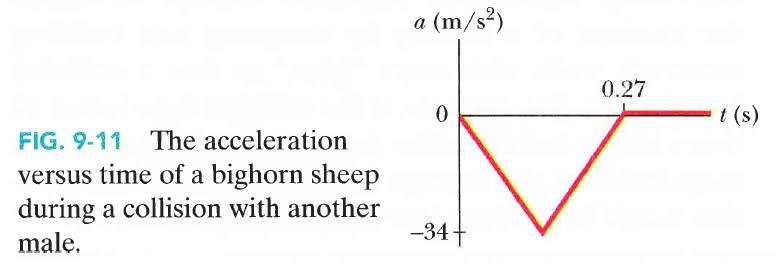
I know impulse is equal to the change in momentum (J = mΔv). So first I found vo by using v = vo + at. After plugging in the numbers, I got vo = -9.18 m/s. I then plugged this into the formula J = mΔv = m(v - vo), where v = 0 m/s, to get 826.2 Ns as the impulse. Unfortunately, the book has exactly half of that as the answer (413 Ns) as the answer. The way they did it was finding the area between the plot and the axis of Figure 9-11, then multiplying it by 90 kg. I understand why this works, but what I don't understand is how my answer comes out to be twice as large.
Any help is greatly appreciated. Thanks.
I know impulse is equal to the change in momentum (J = mΔv). So first I found vo by using v = vo + at. After plugging in the numbers, I got vo = -9.18 m/s. I then plugged this into the formula J = mΔv = m(v - vo), where v = 0 m/s, to get 826.2 Ns as the impulse. Unfortunately, the book has exactly half of that as the answer (413 Ns) as the answer. The way they did it was finding the area between the plot and the axis of Figure 9-11, then multiplying it by 90 kg. I understand why this works, but what I don't understand is how my answer comes out to be twice as large.
Any help is greatly appreciated. Thanks.