jackrc11
- 6
- 0
Given a charged sphere, the electric field within it is zero at every point. Why is this? Why is not merely zero only at the center? If a sphere is conducting, then its charge is all across the surface. If electric field is inversely proportional to distance from charge squared, won't the field be greater at a point that isn't in the center, as it will be closer to one side of the sphere?
My attempt to visualize this question: http://[PLAIN]http://i.imgur.com/nhvZjNh.png
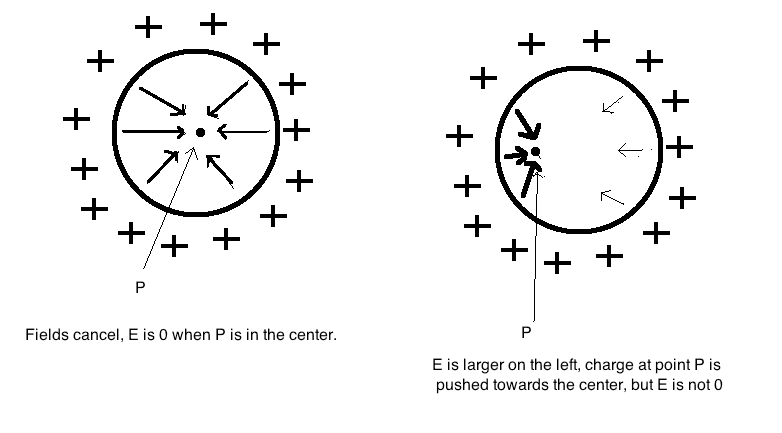
My attempt to visualize this question: http://[PLAIN]http://i.imgur.com/nhvZjNh.png
Last edited by a moderator: