werson tan
- 183
- 1
Homework Statement
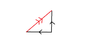
why the resultant force on blade is acted downwards (toward A)? why shouldn't it be slanted upwards ?
since the horizontal component of the force acted 2.12kN to the left , and 0.735kN upwards , we would get the resultant force acting slanted upwards , right ?