Why is the second approach incorrect? pulley problem

[EastWindBreaks]

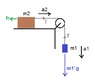
Homework Statement

Homework Equations

friction force = F_v
m=m1

The Attempt at a Solution

is method 1 correct? if so, why method 2 came out with a totally incorrect answer.
I understand that you can also set up acceleration equations for m1 and m2, since their acceleration are equal, and solve the system of equation. I am just curious if I can do it by force components. [/B]

 

[Chandra Prayaga]

I actually have a question about your method 1. You are taking mg, which is in the y direction, and F_v, which is in the x direction, and just adding them as algebraic quantities. How are you able to do that? Does that not say that method 1 is wrong?

 

[EastWindBreaks]

I actually have a question about your method 1. You are taking mg, which is in the y direction, and F_v, which is in the x direction, and just adding them as algebraic quantities. How are you able to do that? Does that not say that method 1 is wrong?

Yes,you can, because in the first method, I am treating the system as a whole(single object), so, only external forces matters.

 

[haruspex]

why method 2 came out with a totally incorrect answer.

First, you need to say exactly what you mean by Fx and Fy.

 

[EastWindBreaks]

First, you need to say exactly what you mean by Fx and Fy.

Hello, I meant Fx as in sum of forces in x direction, Fy as sum of forces in y direction

 

[haruspex]

Hello, I meant Fx as in sum of forces in x direction, Fy as sum of forces in y direction

Sum of forces on what system?

 

[EastWindBreaks]

Sum of forces on what system?

on the entire pulley system

 

[EastWindBreaks]

Sum of forces on what system?

I guess Ft-Fv=(m1+m2)*a and m1g-Ft=(m1+m2)*a as well, equating them would be sufficient? since they have same acceleration.

 

[haruspex]

on the entire pulley system

Two masses plus string? ... plus pulley? ... plus bench?
Whichever you pick, you are missing some external forces in your equation.

 

[ehild]

Write Newton's second law separately for the masses. The hanging mass moves in the vertical (y) direction, with vertical acceleration a₁, The sliding mass moves in the horizontal direction with horizontal acceleration a₂. The tension in the rope is T, the same everywhere. So m₁a₁= m₁g -T
m₂a₂ = T-fr.
As the length of the rope is constant, the magnitude of the accelerations are the same a₁=a₂=a. We can consider a as the acceleration along the rope, making the problem one-dimensional. Adding the equations above, the tension cancels, and you get the acceleration in terms of the external forces /gravity, friction) and the sum of the masses.

 

[Chandra Prayaga]

The problem in the second method is that you are first writing the equation of motion for each mass, and then taking the forces on the different masses as a single force with x and y components. That gives you your equation
√(F_x² + F_y ²) = a (m₁ + m₂)
This is wrong because you now have a force on the left with some weird direction, and an acceleration on the right, which is either horizontal or vertical (they are the same).

 

[EastWindBreaks]

The problem in the second method is that you are first writing the equation of motion for each mass, and then taking the forces on the different masses as a single force with x and y components. That gives you your equation
√(F_x² + F_y ²) = a (m₁ + m₂)
This is wrong because you now have a force on the left with some weird direction, and an acceleration on the right, which is either horizontal or vertical (they are the same).

wow, right on the point! that makes sense now. thank you!

 

[ehild]

The problem in the second method is that you are first writing the equation of motion for each mass, and then taking the forces on the different masses as a single force with x and y components. That gives you your equation
√(F_x² + F_y ²) = a (m₁ + m₂)
This is wrong because you now have a force on the left with some weird direction, and an acceleration on the right, which is either horizontal or vertical (they are the same).

If all the external forces are added vectorially, and the sum is divided by the whole mass, it gives the acceleration of the center of mass. Among the external force is also the force the pulley acts on the system of two masses connected by the rope.