Why is the Thevenin resistance in this problem 3.2 kΩ?

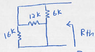
[s3a]

Homework Statement

The problem and its solution are attached.

Homework Equations

"Steps to follow for Thevenin’s Theorem:
(1) Find the Thevenin source voltage by removing the load resistor from the original circuit and calculating voltage across the open connection points where the load resistor used to be.
(2) Find the Thevenin resistance by removing all power sources in the original circuit (voltage sources shorted and current sources open) and calculating total resistance between the open connection points.
(3) Draw the Thevenin equivalent circuit, with the Thevenin voltage source in series with the Thevenin resistance. The load resistor re-attaches between the two open points of the equivalent circuit.
(4) Analyze voltage and current for the load resistor following the rules for series circuits."

- https://www.allaboutcircuits.com/textbook/direct-current/chpt-10/thevenins-theorem/

The Attempt at a Solution

If one replaces the voltage sources with a short circuit, wouldn't that mean that the current ignores the 6 kΩ resistor and that R_ab = 12*16/(12+16) = 6.85714285714285714286 kΩ, instead of 3.2 kΩ?

Could someone please let me know whether I'm right or wrong? If I'm wrong, I'd appreciate having an explanation as to why I'm wrong, as well.

 

[willem2]

I have no idea why you think that "the current ignores the 6k resistor". If you replace the voltage sources with short circuits you get the circuit you've drawn at the bottom left of the PDF. There will certainly be current through the 6k resistor, and the calculation that produces a 3.2kΩ resistance is correct.

 

[phinds]

I have no idea why you think that "the current ignores the 6k resistor". If you replace the voltage sources with short circuits you get the circuit you've drawn at the bottom left of the PDF. There will certainly be current through the 6k resistor, and the calculation that produces a 3.2kΩ resistance is correct.

+1 on that

 

[s3a]

I think that because, for this other problem (attached in this post), the two top 2 Ω resistors seem to be ignored by the short circuit. And, the reason I feel that the short circuit means "ignore the other branch(es)" is because, in theory, it has a resistance of 0 Ω, so all the current would "want" to go from that path. At least that's how I justified understanding these notes (attached in this post) from class. Basically, I can't think of a common way to explain the solution to both problems.

 

[phinds]

I think that because, for this other problem (attached in this post), the two top 2 Ω resistors seem to be ignored by the short circuit. And, the reason I feel that the short circuit means "ignore the other branch(es)" is because, in theory, it has a resistance of 0 Ω, so all the current would "want" to go from that path. At least that's how I justified understanding these notes (attached in this post) from class. Basically, I can't think of a common way to explain the solution to both problems.

Yeah, that's probably because you drew the short circuit in this problem as an OPEN circuit and thus have done it incorrectly

 

[s3a]

Yeah, that's probably because you drew the short circuit in this problem as an OPEN circuit and thus have done it incorrectly

Isn't there supposed to be both an open and short circuit introduced in the handwritten problem? Are you only looking at the current source's replacement? (There's also a voltage source that was replaced.)

 

[phinds]

Isn't there supposed to be both an open and short circuit introduced in the handwritten problem? Are you only looking at the current source's replacement? (There's also a voltage source that was replaced.)

Yes, but also this problem is not the same, so your comparison between the two problems is not valid

 

[s3a]

View attachment 228229
Yes, but also this problem is not the same, so your comparison between the two problems is not valid

What about them differs, though?

 

[phinds]

What about them differs, though?

the current source and the corresponding open circuit. Can you not see how an open circuit is different that a short circuit?

 

[s3a]

Yes, but when one removes a current source, it's like nothing is there, and when one removes a voltage source, a wire is still there (without the voltage source), and both problems' simplified circuits for finding R_Thevenin have wires with resistors and at least one wire with nothing.

I guess my main question is: How do/does the wire(s) with nothing change the behaviour of the circuits?

If I try to think like in the problem with the 3.2 kΩ answer, I get 2 Ω + 2 Ω + 4 Ω = 8 Ω (instead of 4 Ω) as the answer for the fully-handwritten problem, and if I try to think like in the fully-handwriten problem I get roughly 6.86 kΩ as the answer to the problem with the 3.2 kΩ answer.

 

[phinds]

... both problems' simplified circuits ... have ... at least one wire with nothing./QUOTE]Really? Where is the "wire with nothing" in the first problem?

 

[s3a]

In the simplified circuit that's below the "To Calculate R_th:" text.

Edit: The vertical line that's a horizontal distance away from the line with the 16 kΩ resistor and below the node that both the 12 kΩ and 6 kΩ resistors are connected to.

 

[phinds]

In the simplified circuit that's below the "To Calculate R_th:" text.

Edit: The vertical line that's a horizontal distance away from the line with the 16 kΩ resistor and below the node that both the 12 kΩ and 6 kΩ resistors are connected to.

OK, you're just talking about a short circuit. I assumed you meant a line that had been removed.

 

[s3a]

Yes; the wire is there and has nothing on it, but it is there. :)

 

[s3a]

Yes, but when one removes a current source, it's like nothing is there, and when one removes a voltage source, a wire is still there (without the voltage source), and both problems' simplified circuits for finding R_Thevenin have wires with resistors and at least one wire with nothing.

I guess my main question is: How do/does the wire(s) with nothing change the behaviour of the circuits?

If I try to think like in the problem with the 3.2 kΩ answer, I get 2 Ω + 2 Ω + 4 Ω = 8 Ω (instead of 4 Ω) as the answer for the fully-handwritten problem, and if I try to think like in the fully-handwriten problem I get roughly 6.86 kΩ as the answer to the problem with the 3.2 kΩ answer.

So, this clarification brings us back to this.

 

[vela]

For a short circuit to take a resistor out of the circuit, it has to be in parallel with the resistor. If the two ends of a resistor are shorted, there's no potential drop across the resistor, so by Ohm's law, there will be no current.

In the original circuit, when you replace the voltage sources by a wire, the two ends of the 6-ohm resistor are not shorted, so current will still flow through it. In the second circuit, the two 2-ohm resistors are in series, so you can replace them with a single 4-ohm resistor. That 4-ohm resistor is in parallel with the short circuit, so no current flows through it.

 

[willem2]

It should be simple to find the resistance of this circuit:

There aren't that many different circuits with 3 resistors, and all of them can be solved with parallel and/or series resistors.
Try redrawing the circuit, so it becomes easier to see which points are now the same.

It's only possible to remove resistors because of short circuits if there's a short circuit between both sides of the resistor.
In your second problem you correctly combined the 2 2Ω resistors to a 4Ω resistor and than removed it, because there was a short circuit from
one side of the resistor to the other side.
If you want to remove the 6k resistor in the first circuit, there must be a continuous path with only wires from one side of the 6k resistor to the other side.
That's not the case here. None of these resistors can be removed.

 

[s3a]

Thanks, guys! That's what I needed to know! :D