lost captain
- 69
- 3
- TL;DR Summary
- Why the change in pressure dP is not taken into account when we calculate the work in an isothermal process?
Let's say we have an isothermal compression, isn't the gass compressed due to the initial pressure plus the increase in pressure? If so why work is being calculated as PdV?
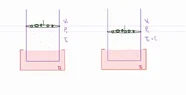
Let's say we have a cylinder of volume V1 with a frictionless movable piston and some gas trapped inside with pressure P1 and temperature T1. On top of the piston lay some small pebbles that add weight and essentially create the pressure P1. Also the system is inside a reservoir of water that keeps its temperature constant at T1.
The system is in equilibrium at V1, P1, T1.
Now let's say i put another very small pebble on top of the piston (0,00001kg)
and after some seconds the system reaches a new equilibrium with
V2<V1 , P2>P1 , T2=T1
What is the work, that has been done to the system?
It s the integral from V1 to V2, in a PV diagram.
What causes the compression, the change in Volume?
Is it the total pressure P1 +dP?
Then shouldn't work be W= (P+dP) × dV and not PdV ?
But then again i don't even understand what dP×dV means. I'm not very advanced in integral calculus maybe that's the reason.
The last part has to do with integral math, I'm sorry if it's not very relevant but i believe it will solve my question to the core :
So I do remember our approach to calculate the area under a graph and that was to "chop" that area in many pieces of dx width and f(x) length and then take the sum of these products, for example one product whould be a specific value f(x1) times the dx of our choice.
Now we have dP times dV, so a change in the function f(x) not a specific value times a change in x?
The system is in equilibrium at V1, P1, T1.
Now let's say i put another very small pebble on top of the piston (0,00001kg)
and after some seconds the system reaches a new equilibrium with
V2<V1 , P2>P1 , T2=T1
What is the work, that has been done to the system?
It s the integral from V1 to V2, in a PV diagram.
What causes the compression, the change in Volume?
Is it the total pressure P1 +dP?
Then shouldn't work be W= (P+dP) × dV and not PdV ?
But then again i don't even understand what dP×dV means. I'm not very advanced in integral calculus maybe that's the reason.
The last part has to do with integral math, I'm sorry if it's not very relevant but i believe it will solve my question to the core :
So I do remember our approach to calculate the area under a graph and that was to "chop" that area in many pieces of dx width and f(x) length and then take the sum of these products, for example one product whould be a specific value f(x1) times the dx of our choice.
Now we have dP times dV, so a change in the function f(x) not a specific value times a change in x?