- #1
mooshasta
- 31
- 0
Recently my AP Physics class had a test on energy. The following is one of the questions verbatim from the test. I just can't work out the problem to any of the choices, let alone the "correct" choice. The problem is:
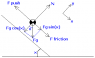
Movers want to set the ramp of their truck so that the work they do against gravity and friction is a minimum for crates moving up the ramp with constant velocity. µ is the coefficient of kinetic friction and x is the angle between the ramp and the ground. For the work to be a minimum, they must choose:
a. tan x = µ
b. tan x = -µ
c. tan x = -1/µ
d. tan x = 1/µ
e. tan x = 1 - µ
My reasoning is as follows:
Since the truck's height is unchanging, the work done against gravity should be constant regardless of the angle of the ramp; work agianst friction is the only variable work. To minimize the work against friction, we should try to minimize the normal force and the actual length of the ramp. The shortest ramp length AND the minimum normal force both occur at x = 90° (this isn't much of a ramp, but oh well). Wouldn't this be the correct answer? The "correct" answer is tan x = 1/µ, but I just don't see how this is possible.
Questions on these tests are often wrong, which is unfortunate.
Thanks in advance,
Andrew
Movers want to set the ramp of their truck so that the work they do against gravity and friction is a minimum for crates moving up the ramp with constant velocity. µ is the coefficient of kinetic friction and x is the angle between the ramp and the ground. For the work to be a minimum, they must choose:
a. tan x = µ
b. tan x = -µ
c. tan x = -1/µ
d. tan x = 1/µ
e. tan x = 1 - µ
My reasoning is as follows:
Since the truck's height is unchanging, the work done against gravity should be constant regardless of the angle of the ramp; work agianst friction is the only variable work. To minimize the work against friction, we should try to minimize the normal force and the actual length of the ramp. The shortest ramp length AND the minimum normal force both occur at x = 90° (this isn't much of a ramp, but oh well). Wouldn't this be the correct answer? The "correct" answer is tan x = 1/µ, but I just don't see how this is possible.
Questions on these tests are often wrong, which is unfortunate.
Thanks in advance,
Andrew