Work done by friction in a system

[Angeee]

Homework Statement

work done by friction=? as big M slides through a distance of 3 meters.
what is the speed of small m when it hits the ground?
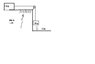
M=5kg m=2kg m is 3meters above ground muk is.25

I can't figure out how to post a drawing (first post)Big M is horizonatal and frictionless b4 muk attached by a string over a pulleyattached by same string to m which is the 3 meters above ground.
2.
Relevant equations

wf = -fkd wf=e2-e1

The Attempt at a Solution

do i use cos180 since it is horizontal and I am lost on part 2

 

[Astronuc]

A picture would be helpful. One could created a gif or bmp file and attach it, or put the image on a site like imageshack or flickr and use tags (roll the cursor over the buttons just above the posting box).


So M is sliding on the horizontal in one direction, and m is pulled over it in the opposite direction at some point. They are connected by a string which passes through/around a frictionless pulley. Is M sliding on a frictionless surface? So then the only friction interaction is between M and m?

If the only friction is between M and m, then one only needs to consider the friction while they are in contact. What is the length of M, i.e. how far does m travel over M?

 

[Angeee]

Ok so far i have work done by friction -36.75 which the cos 180 just gives me the negative.

and the speed of small m=6.1 m/s
using the eq-----mk*mgd=mgh2+1/2mv^2-mgh1
am I on the right track?
I feel like i have missed some steps?

 

[Astronuc]

The work done by friction is correct. 36.75 J is lost due to friction.

The velocity seems a bit high.

See if this helps - http://hyperphysics.phy-astr.gsu.edu/hbase/hpul2.html#c1

In using the eq-----mk*mgd=mgh2+1/2mv^2-mgh1, one must include the kinetic energy of M, and don't forget to distinguish between m and M.

 

[Angeee]

Thank you-I like the link you sent. Looks like I need to still take the square root of the 6.3 which makes the correct answer...2.51m/s.