Simon Goster
- 4
- 0
1. The Question
Unable to find the work done by spring on the object sliding down the rod as shown below:
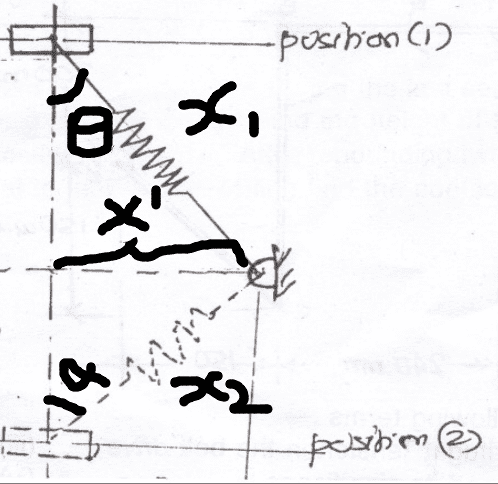
Work Done by Spring Force : -1/2 * KΔx2 --(1)
where k = Spring Constant
Δx = Change in Spring Length[/B]
3. Where the problem occurred
While seeing the solution of the problem, it was mentioned that we can simply take
WSpring = -1/2 * K(X22-X12) --(2)
But my problem is that if the position of ring on rod is changing, the angle of spring with the rod is changing and thus the force components on rod is changing, then how the usual formula
Work Done by Spring Force : -1/2 * KΔx2
is also valid for the given condition.
PS: I also tried to understand this using concept of conservative force, but couldn't get it.
Thanks!
Unable to find the work done by spring on the object sliding down the rod as shown below:
Homework Equations
Work Done by Spring Force : -1/2 * KΔx2 --(1)
where k = Spring Constant
Δx = Change in Spring Length[/B]
3. Where the problem occurred
While seeing the solution of the problem, it was mentioned that we can simply take
WSpring = -1/2 * K(X22-X12) --(2)
But my problem is that if the position of ring on rod is changing, the angle of spring with the rod is changing and thus the force components on rod is changing, then how the usual formula
Work Done by Spring Force : -1/2 * KΔx2
is also valid for the given condition.
PS: I also tried to understand this using concept of conservative force, but couldn't get it.
Thanks!
Last edited: