AtlBraves
- 11
- 0
I can not figure out what I am doing wrong for this problem. Right now I have Wt = 60*.3*cos(50) = 12 J. If that is taken away, then it should be a 12 J difference right?
In Figure 7-33, a block of ice slides down a frictionless ramp at angle = 50°, while an ice worker pulls up the ramp (via a rope) with a force of magnitude Fr = 60 N. As the block slides through distance d = 0.30 m along the ramp, its kinetic energy increases by 80 J. How much greater would its kinetic energy have been if the rope had not been attached to the block?
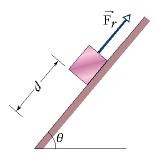
In Figure 7-33, a block of ice slides down a frictionless ramp at angle = 50°, while an ice worker pulls up the ramp (via a rope) with a force of magnitude Fr = 60 N. As the block slides through distance d = 0.30 m along the ramp, its kinetic energy increases by 80 J. How much greater would its kinetic energy have been if the rope had not been attached to the block?