victoration1
- 7
- 0
Homework Statement
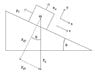
A girl uses a 3.0 m long ramp to push her 110 kg motorbike up to a trailer, the floor of which
is 1.2 m above the ground. How much work is done on the motorbike?
Homework Equations
W=FD where W is work, F is force and D is distance travelled.
The Attempt at a Solution
Assuming that 3.0m long ramp means a base length of 3.0 meters, then the hypotenuse of the ramp must be approximately 3.2meters. Thus, the bike must travel 3.2 meters in a diagonal direction. What I cannot find is the force which will push this bike up the ramp.