Work & energy VS conservation of angular momentum

[Ebi]

Summary:: Would energy method give us a different answer from conservation of angular momentum?

Hello,

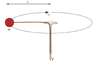
I do not know how to type equations here. So, I typed my question in Word and attached it here. Please see photos.

Note: This question is not a homework. I did not find it in textbooks or websites, it was designed by me.
Thank you.

 

[jbriggs444]

Can you show your work? I do not see that the force integral has been evaluated.

 

[Ebi]

F is variable F=mrω^2, so I did not calculate it. It seems the two answers are different.

 

[A.T.]

F is variable F=mrω^2,

That's the centripetal force for uniform circular motion, which is not your scenario.

It seems the two answers are different.

To show that the answers for w₂ are different, you have to solve for w₂ with both approaches.

 

[jbriggs444]

That's the centripetal force for uniform circular motion, which is not your scenario.

In particular, you are integrating $F(r) dr$ to get $\omega(r)$. But using $\omega(r)$ to get $F(r)$. That strikes me as a valid approach. But you have to solve the differential equation.

 

[Ebi]

In particular, you are integrating $F(r) dr$ to get $\omega(r)$. But using $\omega(r)$ to get $F(r)$. That strikes me as a valid approach. But you have to solve the differential equation.

Thanks for your responses.
In that case, $\omega(r)$ and $F(r)$ would also be unknown. Such differential equation would be derivative of the work-energy equation above. Or I'm missing something?

 

[Ebi]

That's the centripetal force for uniform circular motion, which is not your scenario.

Thanks for your response.
If we suppose the string is pulled slowly ( quasi-statically), F is F=mrω^2 +dF
Do you have a breakthrough to F(r)?

 

[jbriggs444]

If we suppose the string is pulled slowly ( quasi-statically), F is F=mrω^2 +dF
Do you have a breakthrough to F(r)?

I am not an expert on this. But let us see how far we can get. Let us start by seeing whether there is a useful relationship between the energy in the object at radius r and the centripetal force on the object at radius r.

If you've never attacked differential equations before, you might give it a try before cracking this open. This is all played fairly without cheating. I picked an approach and worked it through in the sequence as given herein without knowing in advance whether it would give the desired result.

Spoiler

Let us write down formulas for energy and force.
$$E(r)=\frac{1}{2}m v^2 = \frac{1}{2}m \omega^2 r^2$$
$$F(r)=m \omega^2r = \frac{2E(r)}{r}$$
The incremental work done by $F(r)$ over distance dr is $F(r)$ multiplied by $dr$. If we write $F(r)$ as $\frac{2E(r)}{r}$ we get incremental work as $\frac{2E(r)}{r} dr$. So we can write:$$dE= \frac{2E(r)}{r} dr$$or$$\frac{dE}{dr} = \frac{2E(r)}{r}$$That is a differential equation. [The above effort was aimed at coming up with a differential equation. The only question was what variable to use -- velocity, angular velocity, energy or something else. I guessed that Energy would be helpful and that guess worked out well].

Now if you knew absolutely nothing about solving differential equations (and after some 40 years out of school, I am pretty much in that boat), you would approach this by trying to find a function that, when you differentiate it once, you wind up with what you started with divided by r.

What about a polynomial function? When you differentiate $r^k dr$ then you get $kr^{k-1}$. That is pretty much the same as dividing by r. We just have to get the constant multiplier (that k in front) right. Here we are aiming to differentiate $r^k$ to get $2r^{k-1}=2\frac{r^k}{r}$. So k = 2 and $E(r) = r^2$ is our solution...

This sure sounds neat. And it even fooled me for a minute. But it contains a sign error. The force is in the opposite direction to increasing r. The incremental work done is a decrement to E(r), not an increment. We need a minus sign in the differential equation like so:$$\frac{dE}{dr} = \frac{-2E(r)}{r}$$So instead of $k=2$ and $r^2$ as a solution we get $k=-2$ and $r^{-2}$ as a solution. Then $-2r^{-3} = \frac{-2r^{-2}}{r}=\frac{-2E(r)}{r}$ is its derivative, just as we planned.

Now then, if energy E is inversely proportional to the square of radius then angular velocity $\omega$ must be inversely proportional to radius. And *SHAZAAM*, that's exactly what the angular momentum calculation calls for.

As is typical for [homogeneous, linear] differential equations, given one solution you can find others by simply multiplying by a constant. If $E(r) = \frac{1}{r^2}$ is a solution then $E(r) = \frac{k}{r^2}$ is also a solution. [And given two or more solutions, any sum of fixed multiples of each is a solution]

You normally solve the equation first, getting the general form of the result then look back at the givens of the problem (the "boundary conditions") to see what constant multiple you need. For instance, if the starting energy at radius 10 meters is 57.5 joules then $E(r) = \frac{57500}{r^2}$ is the desired result.

I do not know how to type equations here.

See the LaTeX guide which is linked to the lower left of the editing pane. Or Info => Help => Learn LaTeX for Math Equations. Both take you to the same page.

If you reply to this post you will see worked examples of stuff like ##E(r) = \frac{1}{r^2}## which is rendered as $E(r) = \frac{1}{r^2}$

 

[Ebi]

I am not an expert on this. But let us see how far we can get. Let us start by seeing whether there is a useful relationship between the energy in the object at radius r and the centripetal force on the object at radius r.

If you've never attacked differential equations before, you might give it a try before cracking this open. This is all played fairly without cheating. I picked an approach and worked it through in the sequence as given herein without knowing in advance whether it would give the desired result.

Spoiler

Let us write down formulas for energy and force.
$$E(r)=\frac{1}{2}m v^2 = \frac{1}{2}m \omega^2 r^2$$
$$F(r)=m \omega^2r = \frac{2E(r)}{r}$$
The incremental work done by $F(r)$ over distance dr is $F(r)$ multiplied by $dr$. If we write $F(r)$ as $\frac{2E(r)}{r}$ we get incremental work as $\frac{2E(r)}{r} dr$. So we can write:$$dE= \frac{2E(r)}{r} dr$$or$$\frac{dE}{dr} = \frac{2E(r)}{r}$$That is a differential equation. [The above effort was aimed at coming up with a differential equation. The only question was what variable to use -- velocity, angular velocity, energy or something else. I guessed that Energy would be helpful and that guess worked out well].

Now if you knew absolutely nothing about solving differential equations (and after some 40 years out of school, I am pretty much in that boat), you would approach this by trying to find a function that, when you differentiate it once, you wind up with what you started with divided by r.

What about a polynomial function? When you differentiate $r^k dr$ then you get $kr^{k-1}$. That is pretty much the same as dividing by r. We just have to get the constant multiplier (that k in front) right. Here we are aiming to differentiate $r^k$ to get $2r^{k-1}=2\frac{r^k}{r}$. So k = 2 and $E(r) = r^2$ is our solution...

This sure sounds neat. And it even fooled me for a minute. But it contains a sign error. The force is in the opposite direction to increasing r. The incremental work done is a decrement to E(r), not an increment. We need a minus sign in the differential equation like so:$$\frac{dE}{dr} = \frac{-2E(r)}{r}$$So instead of $k=2$ and $r^2$ as a solution we get $k=-2$ and $r^{-2}$ as a solution. Then $-2r^{-3} = \frac{-2r^{-2}}{r}=\frac{-2E(r)}{r}$ is its derivative, just as we planned.

Now then, if energy E is inversely proportional to the square of radius then angular velocity $\omega$ must be inversely proportional to radius. And *SHAZAAM*, that's exactly what the angular momentum calculation calls for.

As is typical for [homogeneous, linear] differential equations, given one solution you can find others by simply multiplying by a constant. If $E(r) = \frac{1}{r^2}$ is a solution then $E(r) = \frac{k}{r^2}$ is also a solution. [And given two or more solutions, any sum of fixed multiples of each is a solution]

You normally solve the equation first, getting the general form of the result then look back at the givens of the problem (the "boundary conditions") to see what constant multiple you need. For instance, if the starting energy at radius 10 meters is 57.5 joules then $E(r) = \frac{57500}{r^2}$ is the desired result.

See the LaTeX guide which is linked to the lower left of the editing pane. Or Info => Help => Learn LaTeX for Math Equations. Both take you to the same page.

If you reply to this post you will see worked examples of stuff like ##E(r) = \frac{1}{r^2}## which is rendered as $E(r) = \frac{1}{r^2}$

Great effort, thank you.
Just, one thing, mass m has a radial velocity as well, I do not see that in the energy equation you wrote. Am I missing something?

 

[jbriggs444]

Great effort, thank you.
Just, one thing, mass m has a radial velocity as well, I do not see that in the energy equation you wrote. Am I missing something?

Quasistatic. The radial velocity is never large. And you end in a circular trajectory where it is entirely absent. So as a contribution to the energy balance, it is not relevant.

The force with which you pull on the string does not depend strongly on radial velocity. So the work you do on the string does not depend strongly on radial velocity. The force does depend strongly on tangential velocity. And the work does depend on the total radial displacement, of course. But not on how rapidly you cover that radial displacement.

In addition, Newtonian mechanics is a consistent system. If you accounted carefully for radial velocity you know that the result would work out exactly and match the predictions based on angular momentum.