Year 12: Cambridge Physics Problem (Oscillatory Motion)

[johnconnor]

A model of the carbon dioxide (CO₂) molecule is constructed as shown in Fig. SM10.1

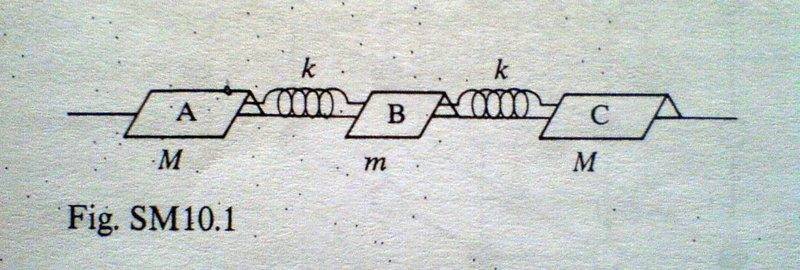
Two sliders A and C, each of mass M, represent the oxygen atoms and are connected by light springs, of force constant k, to a slider B of mass m, representing the carbon atom. All three sliders are placed on a linear air track. The two important modes of oscillation along the axis of the model molecule are as follows:
Mode 1: B remains stationary, and A and C oscillate so that the centre of mass of the model molecule remains stationary
Mode 2: A and C move equal distances in one direction, and B moves in the opposite direction in such a way that the centre of mass again remains stationary.

Show that the frequency f of mode 2 is given by f = (1/2\pi) [(k/M) + (2k/m)]^{1/2}

Attempt:

Forgive me for my messy working:
\text{In\ equilibrium,} zm = M (2y)

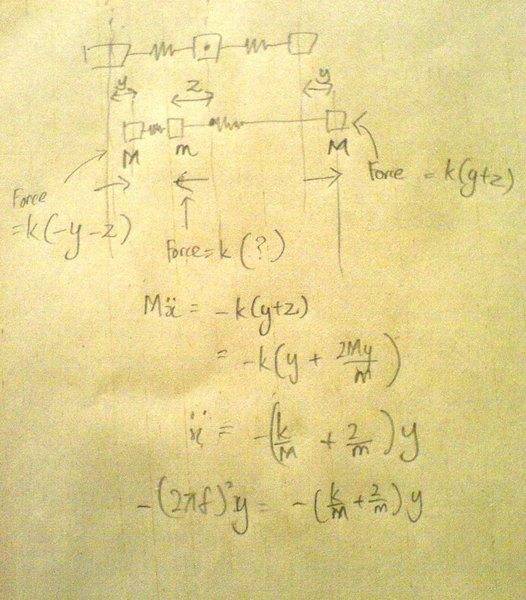
I came to me that the centre of mass of the system should remain unchanged throughout the motion, but how exactly do I justify the statement? Can I say "because there is no net force acting on the system, the centre of mass remains the same throughout the motion"?

Also, I am able to obtain the about equation f if I consider the motion in C. Could someone please show me how to obtain the same equation using B?

Can anybody explain to me how

in equilibrium, zm = M (2y)

actually came about?

Thank you!

 

[Sleepy_time]

Hi johnconnor. So if we consider the motion of mass b: the force acting on b will be m\ddot{x}_b=k{\Delta}x_{ab}+k{\Delta}x_{bc}. You can find the extension and direction of the force by considering displacing a slightly, and displacing b a very large distance in the same direction, the extension of this would be {\Delta}x_{ab}=x_b-x_a and is directed against x_b, therefore: F_{ab}=-k(x_b-x_a). Use a similar approach to determine the effects of c on b. The position of the centre of mass of the system is just R=\frac{Mx_a+mx_b+Mx_c}{2M+m}=0. Using the fact that x_a=x_c for mode 2 for the centre of mass equation will give zm=2My and for the equation of motion of b along with zm=2My will give the SHM equation where you should be able to see what the angular frequency of mode 2 will be.

 

[johnconnor]

You can find the extension and direction of the force by considering displacing a slightly, and displacing b a very large distance in the same direction, the extension of this would be {\Delta}x_{ab}=x_b-x_a and is directed against x_b, therefore: F_{ab}=-k(x_b-x_a).

As in displacing "a" and "b" both to the left, but only the displacement of "b" is much greater than "a"? Isn't that contradictory to mode 2? Assuming that "a" is displaced slightly to the right, and "b" is displaced more to the left, then why is that {\Delta}x_{ab}=x_b-x_a?

Use a similar approach to determine the effects of c on b. The position of the centre of mass of the system is just R=\frac{Mx_a+mx_b+Mx_c}{2M+m}=0.

Don't you need a reference point to calculate centre of mass of a composite object? If we take moments at the LHS of A, then how is that the equation R=\frac{Mx_a+mx_b+Mx_c}{2M+m} equals zero? Please point out what I'm missing out over here.

Using the fact that x_a=x_c for mode 2 for the centre of mass equation will give zm=2My and for the equation of motion of b along with zm=2My will give the SHM equation where you should be able to see what the angular frequency of mode 2 will be.

Similarly, where did the "z" come from? Up to now we've considered x_{ab}, x{bc} etc, but never once a "z"...

 

[Sleepy_time]

As in displacing "a" and "b" both to the left, but only the displacement of "b" is much greater than "a"? Isn't that contradictory to mode 2? Assuming that "a" is displaced slightly to the right, and "b" is displaced more to the left, then why is that {\Delta}x_{ab}=x_b-x_a?

I suggested this method for a way of figuring the forces on any mass due to a spring regardless of which mode/modes it is in. Because from this it gives a general 2nd order differential equation of motion for the mass, in solving, integration constants will appear which are determined by the initial conditions of the system which decide whether it'll be 1st mode, 2nd mode or a linear sum of both. Using this method it doesn't matter which way you extend the masses or which is extended the most, it will give the same answer for the force (it's just a hypothetical situation, the displacement of each spring can be anything). It is just easier if you extend one slightly and the other a large displacement.

Don't you need a reference point to calculate centre of mass of a composite object? If we take moments at the LHS of A, then how is that the equation R=\frac{Mx_a+mx_b+Mx_c}{2M+m} equals zero? Please point out what I'm missing out over here.

Trying to remember how I arrived at that. I'm not to sure, I'll come back to you on that one.

Similarly, where did the "z" come from? Up to now we've considered x_{ab}, x{bc} etc, but never once a "z"...

y and z are just the displacement of the masses for the specific situation of mode 2, so x_a=x_c=y and x_b=z, for mode 2.

 

[johnconnor]

Anyone with any comments? Thank you!

 

[Infinitum]

I came to me that the centre of mass of the system should remain unchanged throughout the motion, but how exactly do I justify the statement? Can I say "because there is no net force acting on the system, the centre of mass remains the same throughout the motion"?

Can anybody explain to me how
zm=M(2y)
actually came about?

Since there is no external force acting on the body, the momentum is conserved. Simply use momentum conservation law on the A-B-C system.

I am able to obtain the about equation f if I consider the motion in C. Could someone please show me how to obtain the same equation using B?

Using the same idea you did in your attempt, you should be able to find the force on B due to the spring. The frequency of B will of course be the same as that of A and C. What would be the force on B? How can you relate this force to the differential equation for SHM?

 

[azizlwl]

Taking moment from the left.
New moment of A,C (move to right)=M_Ay + M_Cy
To maintain equilibrium m_B has to move to the left in equal moment.
mz=2My

 

[johnconnor]

By considering the forces acting on B by masses A and B, I am able to come up with the formula F=k(y+z). However by doing that I am ignoring the forces on the right, and that the formula I obtained at the end is divided by a factor of surd 2. What am I doing wrong over here?
Can somebody please show me a partial solution for this one? I gave been really busy and I'm WAAAAY behind my schedule. Thank you...!

 

[Infinitum]

By considering the forces acting on B by masses A and B, I am able to come up with the formula F=k(y+z). However by doing that I am ignoring the forces on the right, and that the formula I obtained at the end is divided by a factor of surd 2. What am I doing wrong over here?
Can somebody please show me a partial solution for this one? I gave been really busy and I'm WAAAAY behind my schedule. Thank you...!

You have made a mistake taking the force on B. Its not k(y+z) but instead, 2k(y+z)