Apashanka das
- 32
- 0
1. The problem statement, all variables and given/known da
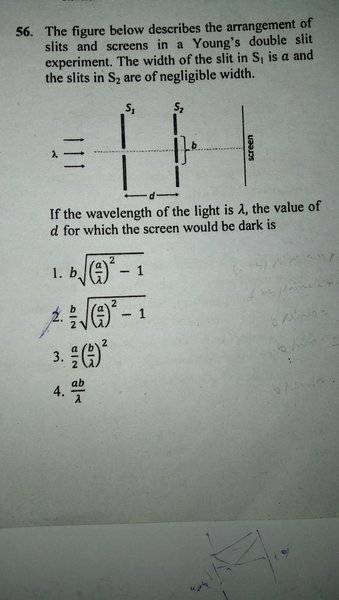
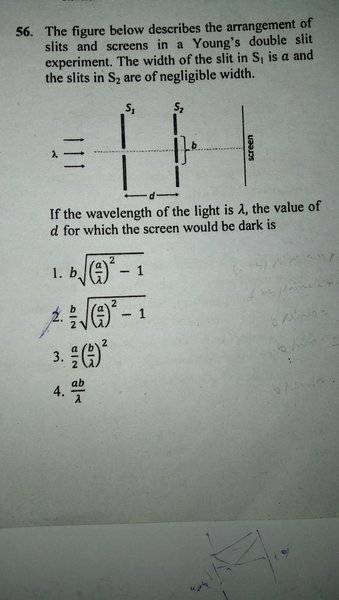
Interference minima is asinΘ=nλ/2 where n=1,3,5,7...
[/B]
Putting ab/(2sqrt(b^2/4+d^2))=λ/2 for first order minima
And solving for d I get (b/2)*sqrt((2a/λ)^2-1) in which only the 2 factor differs in front of a in the square root
from the correct ans which is option 2 in the question
I may be wrong but where I didn't get it?
Homework Equations
Interference minima is asinΘ=nλ/2 where n=1,3,5,7...
[/B]
The Attempt at a Solution
Putting ab/(2sqrt(b^2/4+d^2))=λ/2 for first order minima
And solving for d I get (b/2)*sqrt((2a/λ)^2-1) in which only the 2 factor differs in front of a in the square root
from the correct ans which is option 2 in the question
I may be wrong but where I didn't get it?
