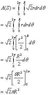I went back and reread the original question. My derivation was assuming that the circular base was in the xy-plane and vertex at (0,0,h). In fact, the tip of the cone is at (0,0,0) and the base of the cone is in the plane z= h. Sorry about that.
This way, it's easier. Look at one side of the cone, in the y= 0 plane. that side is a line from (0,0,0) to (R,0,h). Since y is always 0 we can write that as z= mx+ b. Since z= 0 when x= 0, 0= m(0)+ b so b= 0. Since z= h when x= R, h= m(R) so m= h/R. That's your "k". z= (h/R)x. Again, rotating around the z-axis, that x becomes the more general "r". z= (h/R)r.
Or, as I said before, we can use 'similar triangles' (and, again, it is easier in this configuration). We have two similar right triangles, one, the whole cone, with vertices at (0, 0, 0), (R, h, 0), and (0,h,0). The smaller triangle, for general r, has vertices at (0,0,0), (0, z, 0) and (r, h, 0). For the larger triangle, the vertical side has length h and the horizontal side has length R. The ratio is h/R. For the smaller triangle, the corresponding sides are of length z and r and the ratio is z/r. Setting those equal, z/r= h/R so z= (h/R)r.