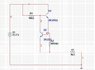
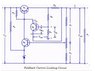
likephysics said:
The pot divider was only for illustrative purpose and maybe a bit of tweaking.
I don't understand how the Ra/Rb divider helps and I also don't know how to find Ra, Rb.
Should I start by fixing the short ckt current? Maybe 1.5A.
You should aim for a smaller short-circuit current (Isc) than 1A, since the maximum current (Ilim) will be larger.
One way to begin the problem would be to decide that you want Ilim to be a certain number N times Isc.
You gave two equations: Ilim = Vbe[(Ra+Rb)/RbRs] +Vout (Ra/RbRs), Isc = Vbe[(Ra+Rb)/RbRs]
Putting Ilim = NIsc, we get Vbe[(Ra+Rb)/RbRs] +Vout (Ra/RbRs) = NVbe[(Ra+Rb)/RbRs]
Vout (Ra/RbRs) = (N-1)Vbe[(Ra+Rb)/RbRs], so Vout/(N-1)Vbe = [(Ra+Rb)/RbRs]/(Ra/RbRs) = (Ra+Rb)/Ra, or Ra = (Ra+Rb)(N-1)Vbe/Vout
Example, N=3, Vout=20V, Vbe=0.6V, using a 1000ohm pot with a 4700 ohm fixed resistor to ground for safety. This would give (Ra+Rb) = 5700ohms
Ra = 5700*(3-1)*0.6/20 = 342 ohms. So Rb = 5700 - 342 = 5358 ohms. (The 1k pot would be set about to about one -third down from the top in your diagram)
It remains to find Rs, in order to get the currents right. Isc = Vbe[(Ra+Rb)/RbRs], so Rs = Vbe[(Ra+Rb)/IscRb]
Isc = Ilim/N, For the example N = 3, Ilim = 1A, Isc = 0.333A, so Rs = 0.6*[(5700)/0.333*5358] = 1.92ohms.
Does this give 1A Ilim as expected? Ilim = Vbe[(Ra+Rb)/RbRs] +Vout (Ra/RbRs), = 0.6*(5700/(5358*1.92) + 20*(342/5358*1.92) = 0.332A + 0.665A = 0.997A
For a practical set-up you could choose Rs to the nearest preferred value, say 1.8ohms or 2ohms. Note it will dissipate 2W for a 1A limit!
Then adjust the R4 pot to set Ilim. Isc won't then be exactly 1/3 of Ilim, but that's probably not very important.