Solve for Equation of Motion in Tricky Mechanics Homework

[JohnSimpson]

Homework Statement

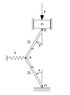
See attached figure. Derive the equation of motion for the following in the parameter \theta

Homework Equations

The Attempt at a Solution

The only part that's giving me trouble is the uppermost massive bar connecting the spring to the mass. I am trying to write down its kinetic energy. I know this can be decomposed as

<br /> T = \frac{1}{2}m\bar{v}^2 + \frac{1}{2}I_{CM}\omega^2<br />

where v-bar is the center of mass velocity and omega is the angular velocity of the body about its CM. I can get the first term, but I can't begin to figure out how to get Omega in the second term. I thought about considering a small change in the position of the mass, as this of course gives rise to a rotation of this bar, but the CM moves during this and it throws me off. Suggestions on how to get Omega, or on an alternative approach would be appreciated.

 

[JohnSimpson]

Hmmm, after another attempt I still can't make heads or tails of finding Omega

 

[tiny-tim]

Hi John!

Hmmm, after another attempt I still can't make heads or tails of finding Omega

?? ω = dθ/dt