Newton's laws - Pedagogical machine

[Saitama]

Homework Statement

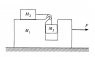
A "Pedagogical machine" is illustrated in the attachment. All surfaces are frictionless. What force F must be applied to $M_1$ to keep $M_3$ from rising or falling?

Ans. clue. For equal masses F=3Mg

Homework Equations

The Attempt at a Solution

I would like to do this problem in both inertial and non-inertial frames but first with the inertial frame.
The net force acting on the system is F. Hence,
F=(M_1+M_2+M_3)a \Rightarrow a=\frac{F}{M_1+M_2+M_3}
Let a' be the acceleration $M_2$ and $M_3$ with respect to $M_1$.
For $M_1$, a normal force (at the point where it is in contact with $M_3$) and a tension acts on it.
F-N-T=M_1a (*)
For $M_2$, $T=M_2(a+a')$
For $M_3$, $M_3g-T=M_3a'$ and $N=M_3a$
Substituting T and N in the equation (*)
F=M_1a+M_3a+M_2a+M_2a'
Solving, $a'=0$. This is obviously wrong.

Any help is appreciated. Thanks!

 

[D H]

Your problem stems from using $F=(m_1+m_2+m_3)a$. This is only true if a'=0, so of course you derived a'=0 as a consequence.

Suppose the rope is cut. The mass m₃ is going to fall to the bottom of the shaft, but while doing so the shaft keeps mass m₃ from moving side-to-side with respect to mass m₁. Thus from a horizontal perspective, if the rope has been cut then $F=(m_1+m_3)\ddot x_1$, where $\ddot x_1$ is the horizontal component of the center of mass of mass m₁. What about mass m₂? It's not a part of the system anymore, at least with regard to horizontal motion. The surface is frictionless, and you don't care about the vertical component of the force on mass m₁.

Now suppose the rope is intact. What horizontal forces, if any, does this add to the m₁+m₃ system? Hint: What does the pulley do?

 

[Tanya Sharma]

Why are you solving for a' ? a' is zero if F is such that M3 doesn't rise or fall.

Considering horizontal direction,for M2 →T=M2a

Considering vertical direction,for M3 →T=M3g

a=(M3g)/M2

For equal masses, a=g and F=3Mg

 

[Saitama]

What horizontal forces, if any, does this add to the m₁+m₃ system?

Tension. It would act in the direction to left. Correct?

Also, I would like to derive the acceleration of individual masses, not only for the case when M3 is not allowed to either rise or fall.

 

[Tanya Sharma]

Hi Pranav :)

What is bothering you in this problem ?

Tension will act leftwards on M1 and rightwards on M2.

 

[Saitama]

Hi Pranav :)

What is bothering you in this problem ?

I don't know but I just can't reach the final answer.
I will write down the equations again.
For $M_1$, $F-N-T=M_1a$.
For $M_2$, $T=M_2(a+a')$
For $M_3$, $N=M_3a$ and $M_3g-T=M_3a'$

Oh well, looks like I get the answer by solving the above equations. I should have been a bit more careful.

Thanks for the help D H and Tanya!

Also, how do I solve this in non-inertial frame?

 

[voko]

Also, how do I solve this in non-inertial frame?

First off, what frame do you think is suitable here?

 

[Tanya Sharma]

Also, how do I solve this in non-inertial frame?

Apply a pseudo force in horizontal direction(opposite to M1) on M2 and M3 and solve just as you would do normally.

 

[WannabeNewton]

Consider the frame with acceleration $a = \frac{F}{M_1 + M_2 + M_3}$. What is the condition that $M_3$ is neither falling nor rising in this frame? It's just that $M_2$ has to be at rest in this frame. Take it from there; it's thankfully very simple.

 

[Saitama]

Consider the frame with acceleration $a = \frac{F}{M_1 + M_2 + M_3}$. What is the condition that $M_3$ is neither falling nor rising in this frame? It's just that $M_2$ has to be at rest in this frame. Take it from there; it's thankfully very simple.

That worked. Thanks WBN!

 

[Avaro667]

Does anyone know what's wrong with my answer for the 2nd part of this exercise?
It says F = 0 and wants the acceleration for M1 .

So here's my analysis, assuming the right be the positive direction for x'x axis and down be positive for y'y axis.

For M2 :

x'x axis : F2 = M2a2

F2 is the rope tension

y'y axis motion is irrelevant .

For M3 :

y'y axis : M3g-F2 = M3a2
x'x axis : -N = M3a1

For M1 :

x'x axis : N-F2 = M1a1
y'y is irrelevant .

N is the normal force acting on M3 by M1 "wall's".

By solving the system i end up with this :

a1 = -[ M1M3/(M1M2 + M1M3 + M2M3 + M3^2) ]*g

It's all good except for the term M2M3 . According to the solution it should be 2M2M3 .
I can't figure out where I'm wrong though . Do i miss something out or is it just the book ?

 

[TSny]

For M3 :

y'y axis : M3g-F2 = M3a2

Is it correct to take the y-component of acceleration of M3 to be equal to the acceleration of M2?

a1 = -[ M1M3/(M1M2 + M1M3 + M2M3 + M3^2) ]*g

It's all good except for the term M2M3 . According to the solution it should be 2M2M3 .

The numerator, M1M3, of your expression for a1 doesn't look right. As M1 goes to infinity, what should the value of a1 approach?

 

[Avaro667]

Is it correct to take the y-component of acceleration of M3 to be equal to the acceleration of M2?

The numerator, M1M3, of your expression for a1 doesn't look right. As M1 goes to infinity, what should the value of a1 approach?

Hey, thanks for checking this out .
M2 and M3 are connected via a rope so,supossing it doesn't expand, those 2 masses should have the same acceleration,right ?

About M1M3 you're right,i miscalculated this part actually,it turns out to be M2M3 .
I still can't get that 2 for that term in dominator though .

 

[TSny]

Hey, thanks for checking this out .
M2 and M3 are connected via a rope so,supossing it doesn't expand, those 2 masses should have the same acceleration,right ?

No, not with respect to the Earth reference frame. (They would have the same acceleration relative to M1.)

For example, what would happen to M3 if M2 were held fixed relative to the Earth while M1 moves to the left?

 

[Avaro667]

No, not with respect to the Earth reference frame. (They would have the same acceleration relative to M1.)

For example, what would happen to M3 if M2 were held fixed relative to the Earth while M1 moves to the left?

So basically i subconsciously changed the reference frame during the analysis for these 2 bodies ?
I'm not sure how to proceed though,too many uknowns,but a few equations only .

 

[TSny]

You have all the equations except for the correct relation between a₁, a₂, and a_3y. See if you can discover that relation.

 

[Avaro667]

You have all the equations except for the correct relation between a₁, a₂, and a_3y. See if you can discover that relation.

I gave it a try and i think i worked this out .
The set of equations i managed to come up with are 5 of them :

F2=M2a2
M3g-F2=M3a3
N-F2=M1a1
-N = M3a1
a1-a2+a3 = 0

Solving gave the correct answer .
Sometimes I'm a bit confused whether 2 objects should have or not the same acceleration . I guess the safest way is to suppose they don't ,unless it's quite obvious,like in the case of M1's and M3's horizontal acceleration a1 ? Thank you so much for helping with this one,much appreciated .