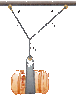intriqet
- 21
- 0
Homework Statement
A bag of cement of weight 350 N hangs from three wires as suggested in the figure below. Two of the wires make angles θ1 = 50.0° and θ2 = 27.0° with the horizontal. Assuming the system is in equilibrium, find the tensions in the wires.
Homework Equations
Newton's Laws of motion
The Attempt at a Solution
I know that the tension for T3 is just equal to the weight. But how do I split the force between the remaining two strings?