Linus Pauling
- 187
- 0
1.
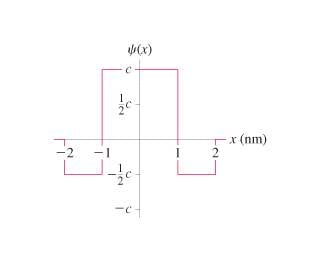
What is c?
2. 1 = integral of wavefunction2 from -infinity to +infinity
3. From the graph, the area above the x-axis is 2/3 the total area. I solved the following integral (int) from -1 to +1:
2/3 = int(c2dx)
Obtaining 2/3 = 2c2
So c = sqrt(1/3) = 0.58 nm-1/2
What is c?
2. 1 = integral of wavefunction2 from -infinity to +infinity
3. From the graph, the area above the x-axis is 2/3 the total area. I solved the following integral (int) from -1 to +1:
2/3 = int(c2dx)
Obtaining 2/3 = 2c2
So c = sqrt(1/3) = 0.58 nm-1/2