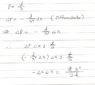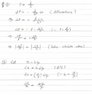Homework about uncertainty principle

[athrun200]

Homework Statement

I don't know how to do 13.10 and 13.11

[PLAIN]http://a367.yahoofs.com/hkblog/LR5wVsiTBB9XH4KDYpBfXDI-_9/blog/20110511014559607.jpg?ib_____DMAbgW2U6

The Attempt at a Solution

I just can't get the answer.
Can you show me the details of the proof and the steps to the answers?

[PLAIN]http://a367.yahoofs.com/hkblog/LR5wVsiTBB9XH4KDYpBfXDI-_9/blog/20110511014542175.jpg?ib_____D8.dLXMZo

 

[Disconnected]

What method are you using to find the uncertainty? Are you using
$$\Delta$$x=SQRT(<x^2>-<x>^2) ?

 

[athrun200]

What method are you using to find the uncertainty? Are you using
$$\Delta$$x=SQRT(<x^2>-<x>^2) ?

I am using($$\Delta$$p)($$\Delta$$x)$$\geq$$reduced Planck constant/2

Can it find the answer?

 

[Disconnected]

I am using($$\Delta$$p)($$\Delta$$x)$$\geq$$reduced Planck constant/2

Can it find the answer?

Well if you are just using the x-p version of the uncertainty relation and not deducing the uncertainty from operators, just sub in!

What is the de broglie relation?

Do you know how to find the error in Y given the error in Z if Y=a/Z, for some constant a?

 

[athrun200]

I know what is de broglie relation.
Can I use the relation like this?
But it seems it is wrong to convert dp to$$\Delta$$p

But I have forgotten how to derive the HUP by using operators.
Can you show me how?

 

[Disconnected]

Well, by operators You simply use the equation I used above for both the x operator and the p operator, then you find their product (and remember that <O>=int(psi*Opsi) ). However, I have no idea what the wavelength operator is. Sorry.

As for the way that uncertainties are added, I'm under the impression that it is by sumsquare, but if there is only one variable...

[tex]\frac{\Delta\lambda}{\lambda}=\frac{\Delta{p}}{p}[\tex]<br /> <br /> Subbing in for p=h/lambda gives<br /> <br /> [tex]\frac{\Delta\lambda}{\Delta{p})=\frac{\lambda^2}{h}[\tex]<br /> <br /> Now if you multiply both sides of the HUP by the relevant side of the above, the h's cancel and it gives<br /> <br /> $$\Delta\lambda\Delta{x}=\frac{\lambda^2}{4\pi}[\tex]<br /> <br /> Which, uh... is out by a factor of 2... So I screwed up somewhere or something?...<br /> Can someone catch my slack here?Edit to add: my tex didn't work. I am actually going to cry soon.$$[/tex][/tex]

 

[BruceW]

On Q13.10 I get it a factor of 2 differently to the book as well. Maybe the book assumes:
$$\Delta x \Delta p > \hbar$$
While we assumed:
$$\Delta x \Delta p > \frac{\hbar}{2}$$
This would mean we get a factor of 2 different to the book.

I think its true you should use:
$$\lambda = \frac{h}{p}$$
And then that means:
$$\frac{\Delta \lambda}{\lambda} = \frac{\Delta p}{p}$$
And now you just use these equations with:
$$\Delta x \Delta p > \frac{\hbar}{2}$$
to get the Heisenberg uncertainty relation in terms of $\lambda$ (by rearranging).
For parts a,b and c, just use the equation they've given you.

For Q13.11, its a bit vague. I think it means you should use
$$\Delta x \Delta p = \frac{\hbar}{2}$$
and assume that a good estimate is given when they are equal, so that:
$$\Delta x = \Delta p = \sqrt{ \frac{\hbar}{2} }$$
(for the initial horizontal momentum and position, and assume no vertical momentum initially).
Using classic equation for uniform horizontal motion:
$$horizontal position = \Delta x + \frac{\Delta p}{m} t$$
At some time t after he dropped it. Then you use the classic expression for vertical distance at a particular time (a is acceleration due to gravity):
$$vertical distance = \frac{1}{2} a t^2$$
and using H as the vertical distance gives the time at which the ball bearing hits the ground. So using this value of t gives the radius of the circle on the floor. Then multiply by 2 to get the diameter:
$$diameter = 2 \Delta x + \frac{2 \Delta p}{m} \sqrt{ \frac{2H}{a} }$$
And now just use the approximate values for $\Delta p$ and $\Delta x$

Alternatively, you could calculate the best possible values of $\Delta p$ and $\Delta x$ to minimise the spread of ball bearings on the floor, but in the question it seems to imply that the guy dropping them doesn't choose the particular values.

 

[lepton5]

I know what is de broglie relation.
Can I use the relation like this?
But it seems it is wrong to convert dp to$$\Delta$$p

But I have forgotten how to derive the HUP by using operators.
Can you show me how?

Hi, athrun, I'm trying to help:

1)i think your start is correct from deBroglie wave, you can take magnitude so negative sign will be gone (check Krane Modern Physics). if you start from p . x > h-bar (no divide by 2) and continue your calculation, it will proof it. But for the calculation, i think the author using h-bar / 2, if you want to get the same result.

2) you can start for (delta p) . (delta x) = h-bar / 2 (u can equal it for the minimum uncertainty), with (delta x) for uncertainty in ball's radius(delta r).
substitute for (delta x) = (delta D)/ 2 and (delta p) = m . (delta v) = m . (delta x)/ (delta t) = m . (delta D)/ 2 (delta t). with D = diameter.
you can simplify the equation to be (delta D)^2 = (2 . h-bar / m ) . delta t, and with (delta t) = sqrt(2 H / g).
Well, it slight different with your book about h there, but if you input it, u will get the same result as the key.

sorry if I'm using word for the equation (i don't know using tex in this forum)...

 

[BruceW]

sorry if I'm using word for the equation (i don't know using tex in this forum)...

This thread explains all you need to know about using latex:
https://www.physicsforums.com/showthread.php?t=386951"
basically, you put (tex) x^2+4 (/tex) but use square brackets [ instead, so it comes out like this $$x^2+4$$

 

[athrun200]

I found somethings interesting.
It seems we can obtain the expression of error from differentiation.

But the question comes. What is the relation between differentiation and error?
It seems they are total different things. So why I can obtain error from differentiation?(see my attachment below.)

Are there any proof?

 

[lepton5]

I found somethings interesting.
It seems we can obtain the expression of error from differentiation.

But the question comes. What is the relation between differentiation and error?
It seems they are total different things. So why I can obtain error from differentiation?(see my attachment below.)

Are there any proof?

Well, you can calculate error (eg: error propagation, relative error) from calculus differential (there is a very close relation between them).
In many types of application, you can used approximation for $$\Delta y \simeq dy$$.

I think in your attachment, you want to calculate relative error from the function y = f(x).
You should consult from your calculus book, there is detail discussion about error and differentiation.
If you get still want to know more, i guess you should post it in calculus thread.