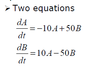You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Analytical solution of these coupled differential equations
- Thread starter gursimran
- Start date
Physics news on Phys.org
- 22,169
- 3,327
"No idea" isn't really an attempt...
What do you know of differential equations? Did you already solve things like this?
What do you know of differential equations? Did you already solve things like this?
HallsofIvy
Science Advisor
Homework Helper
- 42,895
- 984
This is your homework problem- obviously your teacher thinks you should know how to do it yourself! Another problem is there there are several different ways to do this (finding eigenvalues and eigenvectors of a matrix or reducing to a single second order equation, or ...) and we have no idea which you have been taught.
gursimran
- 35
- 0
My teacher dinnt give me this. I figured out this on internet. I'm bad in differential equations. I thought these coupled diff equations can be solved simultaneously and then integration but no such luck cos of one being exactly opp of other ..
- 22,169
- 3,327
gursimran said:My teacher dinnt give me this. I figured out this on internet. I'm bad in differential equations. I thought these coupled diff equations can be solved simultaneously and then integration but no such luck cos of one being exactly opp of other ..
First read http://en.wikipedia.org/wiki/Matrix_exponential then, the interesting part is the section of "applications" which solves a problem very much like yours!
hunt_mat
Homework Helper
- 1,816
- 33
Or failing matrix exponentiation, you can decouple them; Differentiate the top equation to find:
<br /> \frac{d^{2}A}{dt^{2}}=-10\frac{dA}{dt}+50\frac{dB}{dt}<br />
Now use the second equation to substitute for dB/dt, this will leave you with a B in your equation which can be gotten rid of by using the first equation. This will leave you with a second order differential equation for A.
<br /> \frac{d^{2}A}{dt^{2}}=-10\frac{dA}{dt}+50\frac{dB}{dt}<br />
Now use the second equation to substitute for dB/dt, this will leave you with a B in your equation which can be gotten rid of by using the first equation. This will leave you with a second order differential equation for A.
gursimran
- 35
- 0
hunt_mat said:Or failing matrix exponentiation, you can decouple them; Differentiate the top equation to find:
<br /> \frac{d^{2}A}{dt^{2}}=-10\frac{dA}{dt}+50\frac{dB}{dt}<br />
Now use the second equation to substitute for dB/dt, this will leave you with a B in your equation which can be gotten rid of by using the first equation. This will leave you with a second order differential equation for A.
oh thanks a lot, this is a much better and simple solution.
Similar threads
- Replies
- 2
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 21
- Views
- 3K
- Replies
- 7
- Views
- 1K
- Replies
- 7
- Views
- 1K
- Replies
- 2
- Views
- 2K
- Replies
- 25
- Views
- 11K
- Replies
- 10
- Views
- 1K
- Replies
- 4
- Views
- 2K
- Replies
- 3
- Views
- 2K
Hot Threads
-
Prove that the integral is equal to ##\pi^2/8##
- Started by Meden Agan
- Replies: 105
- Calculus and Beyond Homework Help
-
Solve this problem that involves induction
- Started by chwala
- Replies: 7
- Calculus and Beyond Homework Help
-
Limit of piecewise function using epsilon delta
- Started by songoku
- Replies: 31
- Calculus and Beyond Homework Help
Recent Insights
-
Insights Thinking Outside The Box Versus Knowing What’s In The Box
- Started by Greg Bernhardt
- Replies: 1
- Other Physics Topics
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 28
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math