The moment about the Cantilever beam

AI Thread Summary
The discussion centers on understanding the forces acting on a cantilever beam, specifically the horizontal force (H) exerted by the wall. It highlights the relationship between vertical force (V) and weight (W), questioning what other forces are needed to balance the system. The conversation also addresses the moments acting on the beam, noting that the expected clockwise moment is countered by specific forces and distances. The forces at the wall are crucial in determining the beam's reaction to loading. Overall, the analysis emphasizes the importance of understanding force interactions in cantilever beam mechanics.
hjkklm
Messages
12
Reaction score
0
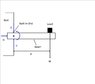
From the picture,
Why do this diagram have the force of H? The wall which exert the force of H to the beam?

V=W that have been known from the questions.
When V=W, what else of other forces to balance the forces of G and H?

Besides, the moment should been clockwise moment, then the counterclockwise in the picture that is occurred by which forces and distance?
:confused:

thank you very much!:smile:
 

Attachments

  • Cantilever beam_1.jpeg
    Cantilever beam_1.jpeg
    10.5 KB · Views: 491
Physics news on Phys.org
The forces at the wall generally denote how the wall reacts to the loaded beam. Therefore only V and the moment would appear.
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »

Similar threads

Vibration of a cantilever beam problem
Replies
2
Views
2K
Deflection of partially loaded cantilever beam with non-homogeneous EI
Replies
3
Views
2K
Moment and force calculation for cantilever beam
Replies
6
Views
11K
Using Macaulay's method of deflection on a cantilever beam
Replies
6
Views
4K
Moment of Inertia: Non Uniform Rod
Replies
1
Views
3K
Engineering Cantilever and encastré beams: bending moment and shear force
Replies
2
Views
3K
Understanding The Concept Of Moments
Replies
6
Views
2K
Moment of inertia of a branched cantilever beam
Replies
7
Views
3K
Beam calculation with 3 unknowns
Replies
5
Views
3K
Angular acceleration of plank hanging off edge with a weight
Replies
7
Views
1K

Hot Threads

Recent Insights

Back
Top